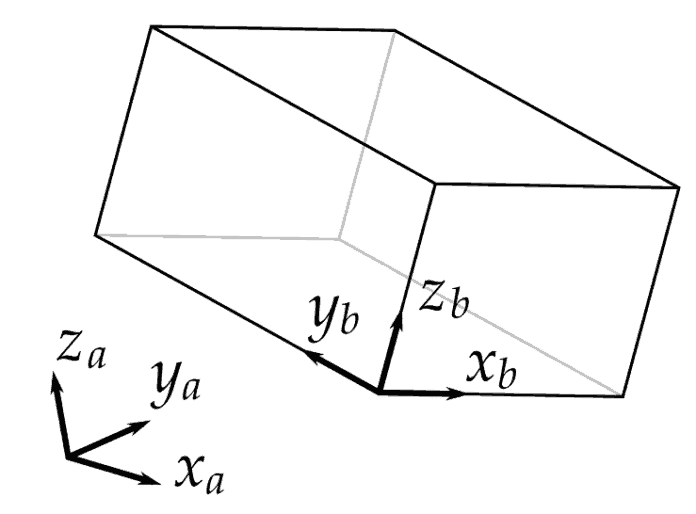
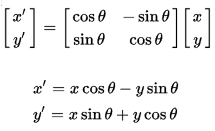Üç boyutlu bir uzayda rijit bir cisim için 3 dönme ve 3 öteleme hareketi olmak üzere toplamda 6 serbestlik derecesi bulunmaktadır. Rijid bir cismin pozisyonunu ve yönünü tanımlamada tercih edilen geleneksel bir yol, ona bir çerçeve eklemektir. Bir referans koordinat sistemi tanımlandıktan sonra, katı gövdenin konumu ve yönü, çerçevenin orijininin konumu ve eksenlerin yönlendirme çerçevesi ile referans çerçeveye göre tam olarak tanımlanır.
Dönme Matrisi (Rotation Matris)
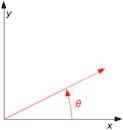
Doğrusal cebirde bir dönme matrisi, Öklid uzayında bir dönüş gerçekleştirmek için kullanılan matristir. Örneğin, iki boyutlu x-y kartezyen düzlemi içerisinde yer alan noktaları koordinat sisteminin orijini etrafında bir θ açısıyla saat yönünün tersine döndürmek için aşağıdaki gibi bir matris kullanılır.
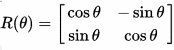
Benzer şekilde üç boyutlu xyz koordinat sistemindeki dönüş hareketi içinde bir dönme matrisi tanımlayabiliriz. Koordinat sistemi eksenlerinden birinin (x, y veya z) etrafındaki dönüşe temel dönüşüm matrisi denir. Aşağıdaki üç temel döndürme matrisi, x, y veya z ekseni etrafında θ açısı ile bir vektörü döndürür.
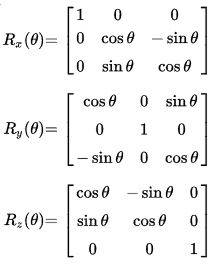
Örneğin x ekseni ile hizalanmış bir vektörü y-eksenine doğru döndürmek için Rz (z ekseninde 90 derecelik dönüş) yapmamız gereklidir. Yani (1,0,0) vektörünü Rz yani z ekseninde 90 derece döndürürsek aşağıdaki gibi bir matris elde ederiz.
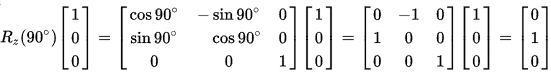
- Selig, J.M., Introductory robotics, Englewood Cliffs (N.J.), Prentice Hall, 1992
- Craig, J.J., Introduction to robotics: mechanics and control, Reading (Mass.), Addison-Wesley, 1986
- Sciavicco L., Siciliano B., Modeling and control of robot manipulators, New York (N.Y.), McGraw-Hill, 1996
- Asada H., Slotine J.-J. E., Robot analysis and control, New York (N.Y.), John Wiley & Sons, 1986