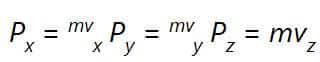Bir golf topuna vurunca ne olacağına bakalım. Çarpışma sonucu topa büyük bir ilk hız kazandırılır. Böylece havada lOOm’den fazla gidebilir ve top büyük bir ivme ile hareket eder. Top bu ivmeyi kısa bir zaman aralığında kazandığından çarpma sonucu üzerine uygulanan kuvvet oldukça büyüktür. Newton’un üçüncü yasasına göre, büyüklüğü sopanın uyguladığı kuvvete eşit ve ters yönde olmak üzere, top da sopa üzerine bir tepki kuvveti uygular. Bu tepki kuvveti de sopaya bir ivme kazandırır. Sopa, topa göre çok büyük olduğundan sopadaki ivmelenme topun ivmelenmesine göre çok küçüktür.
Bu yazının temel amaçlarından biri, böyle olayları anlamak ve çözümlemektir. İlk adım olarak, hareket halindeki cisimlerin açıklanmasında Newton kanunlarının uygulanmasında kolaylık sağlayan momentum kavramını tanımlarız. Kütlesi büyük bir futbolcunun sahada koşarken büyük bir momentuma sahip olduğu söylenir. Daha küçük kütleli bir futbolcu ise büyük bir hızla koşması halinde ancak böyle bir momentum kazanabilir. Bu gerçek, momentumun kütle ile hızın çarpımı olduğunu ortaya koyar. Momentum kavramı, ikinci bir korunum yasasına, momentum korunumuna götürür. Bu yasa, cisimler arasındaki çarpışma problemlerinde ve roket hareketinin analizinde özellikle kullanışlıdır. Ayrıca, bir parçacıklar sisteminin kütle merkezi kavramı tanımlanmakta ve göreceğizki, bir parçacıklar sisteminin hareketi, kütle merkezine konulan temsili bir parçacığın hareketi olarak betimlenebilir.
Önceki yazılarda, Newton yasaları ile kolayca çözümlenemeyecek kadar karmaşık durumlar incelenmişti. Aslında Nevvton da, karmaşık durumlara kolayca uygulanabildiğinden ikinci kanunu olan XF = ma. biçimindeki (5.2) Eşitliğinden az farklı olan bir biçimini kullandı. Fizikçiler, atomik büyüklükteki parçacıklardan roket problemine kadar her konuda bu biçimi kullanırlar. Böyle durumlarda bir cismin kendisi ile hareketi hakkında bilgi sahibi olmak yararlı olur. Şimdi bu durumu ortaya koyan yeni bir kavramı tanımlıyoruz:
v hızı ile hareket eden m kütleli bir parçacığın doğrusal (çizgisel/lineer) momentumu kütle ve hızın çarpımı olarak tanımlanır:
p= mv
Bir m skaleri ile bir v vektörünün çarpımına eşit olduğundan, momentum vektörel bir niceliktir. Yönü, hız ile aynıdır ve boyutu ML/T dir. Sl’de birimi, kg-m/s’dir.
Bir parçacık rastgele bir yönde hareket ediyorsa, p üç bileşene sahip olur ve yukarıdaki eşitliği bileşenleri cinsinden
eşitliklerine denktir. Bu tanımlamadan görüleceği gibi momentum kavramı, aynı hızla hareket eden ağır ve hafif parçacıklar arasında nicel bir farklılığı ortaya koyar. Örneğin, 10 m/s hızla giden bir bovling topunun momentumu, aynı hızda giden bir tenis topunun momentumundan daha büyüktür. Newton, mv çarpımına hareket miktarı demişti. Bu belki de şimdi kullandığımız Latince-den gelen momentum sözcüğünden daha grafiksel bir tasvirdi.
Newton’un ikinci hareket yasasını kullanarak, bir parçacığın doğrusal (çizgisel/lineer) momentumunu ona etki eden kuvvete bağlayabiliriz: Bir parçacığın doğrusal momentum unun değişme hızı (zamana göre türevi) parçacığa etkiyen net kuvvete eşittir:
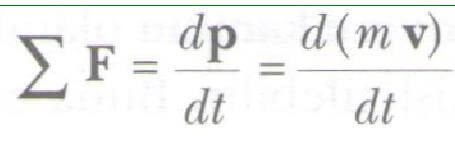
Hız vektörünün zamanla değişmesi durumuna ek olarak, kütlenin de değişmesi durumunda 9.3 Eşitliğini kullanabiliriz. Bir parçacık üzerine etkiyen net kuvvet sıfır olduğu zaman, momentumun zamana göre türevi de sıfır olur ve dolayısı ile doğrusal momentum sabit kalır.1 Eğer parçacık yalıtılmışsa o zaman IF = 0 şartından p sabit olur, bu da p’nın korunduğu anlamına gelir. Karışık hareket problemlerinin çözümünde, enerji korunumu yasası kadar, momentumun korunumu yasası da yararlı olur.
İki Parçacıklı Bir Sistem İçin Momentumun Korunumu
Birbirleriyle etkileşen, çevrelerinden yalıtılmış iki parçacık ele alalım (Şekil 3-2 9.1). Yani, parçacıklar birbirine kuvvet uygulasın fakat hiç bir dış kuvvet bulunmasın. Bu durumun analizinde Newton’un üçüncü kanunu önemlidir. Birinci parçacık ikinci parçacığa bir kuvvet uygularsa (çekim kuvveti olabilir), ikinci parçacık da birinciye büyüklükçe eşit zıt yönde bir kuvvet uygular.
Bir an için, 1. parçacığın momentumunun p2 ve 2. parçacığmkinin p2 olduğunu varsayalım. Her parçacığa Newton’un 2. yasasını uygularsak şöyle yazabiliriz:
Burada F ikinci parçacık tarafından birinciye, F12 ise birinci parçacık tarafından İkinciye uygulanan kuvvettir. Nevvton’un üçüncü yasasına göre F,2 ve F21 kuvvetleri büyüklükçe eşit ve zıt yönlüdür. Bunlar, F)2 = -F21 şeklinde etki-tep-ki çifti oluşturur. Bu durumu
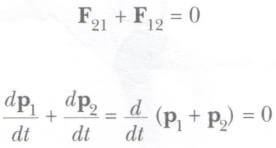olarak yazabiliriz. Toplam momentumun ptop=p1 + p2 zaman göre türevi sıfır olduğundan, sistemin toplam momentumunun sabit kaldığı sonuca varırız.
Kaynak: Serway Kitabı