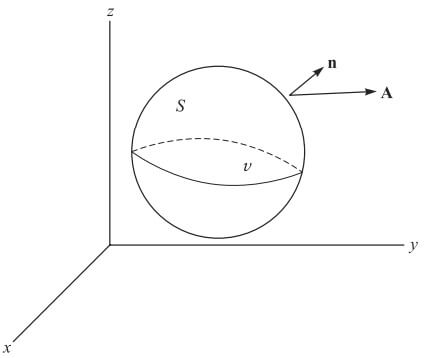
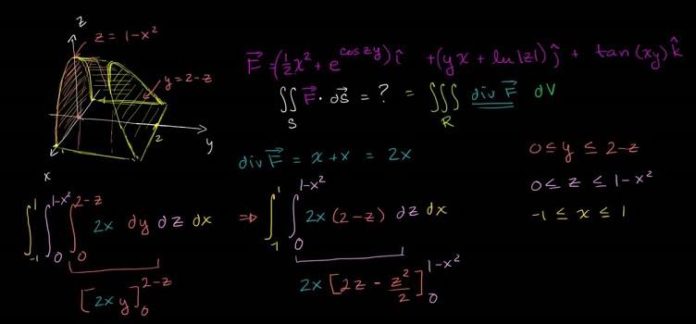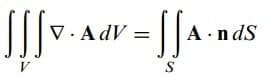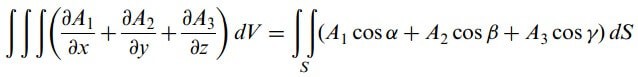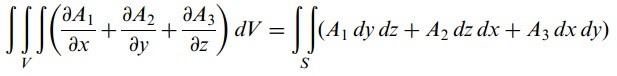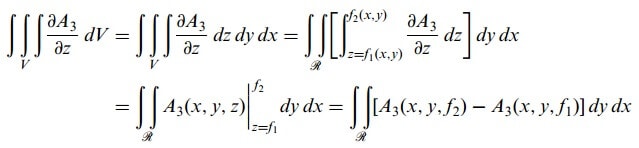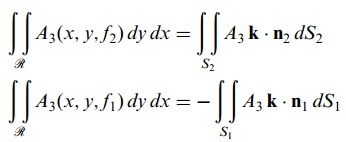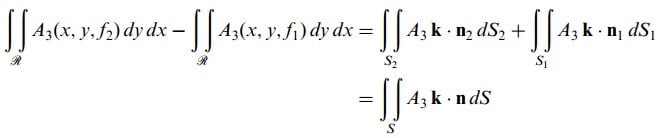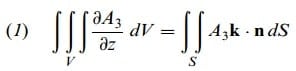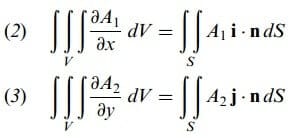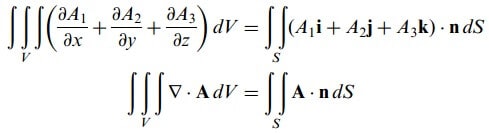Merhaba arkadaşlar bu yazımızda yüzey integrallerinden olan, diverjans teoremi ve konuyu daha iyi kavramanız için diverjans teoremi ispatını sizlere yaptım. Diverjans teoremi, ıraksama teoremi veya gauss teoremi olarak adlandırılır, bir A vektörünün normal bileşeninin kapalı bir yüzey üzerinde alınan integralinin, A nın ıraksamasının bu yüzey tarafından sınırlanan hacim üzerinde alınan integraline eşit olduğunu ifade eder.
A = A1i + A2j + A3k ve n = cosαi + cosβj + cosγk vektör gösterimiyle bu formüller
olarak yazılabilir.
S, V hacimli bir bölgeyi sınırlayan kapalı bir yüzey olsun. Yüzeyin dışa doğru çizilen normali pozitif normal seçilsin ve α, β, γ, sırasıyla, bu normalin pozitif x, y, ve z eksenleriyle yaptığı açılar olsun. O zaman eğer A1, A2, A3 bölgede sürekli ve sürekli kısmı türevlere sahip ise
geçerli olur. Bu
olarak da yazılabilir.
Diverjans Teoremi İspatı
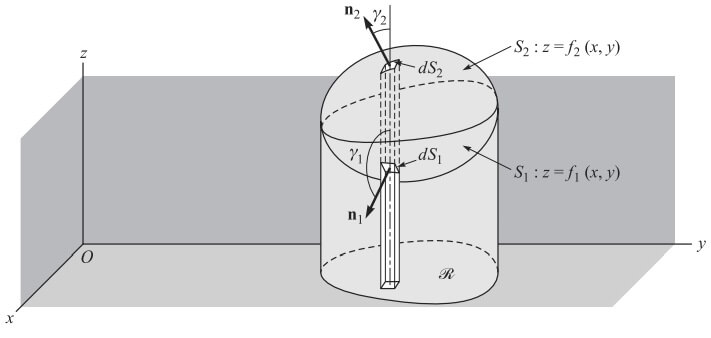
S, koordinat eksenlerine paralel herhangi bir doğru tarafından en çok iki noktada kesilen kapalı bir yüzey olsun. Alt ve üst parçaları olan S1 ve S2 nin denklemleri, sırasıyla, z = f1(x,y) ve z = f2 (x,y) olsun. Yüzeyin xy düzlemi üzerindeki izdüşümü R ile gösteriniz.
integralini düşünelim. S2 nin n2 normali k ile γ2 dar açısını yaptığından, S2 üst parçası için dydx = cosγ2dS2 = kn2dS2
S1 in n1 normali k ile γ1 geniş açısını oluşturduğundan, S1 alt parçası için dydx = -cosγ1dS1 = -kn1dS1 geçerlidir.
Bu taktirde,
Benzer şekilde, S nin diğer koordinat düzlemlerine izdüşümleri için
bulunur.
(1), (2) ve (3) toplanarak
bulunur.
Kısaca özetlemek gerekirse, diverjans teoremi herhangi bir vektör alanı A nın diverjansının, kapalı bir hacimdeki, hacim integralinin aynı vektör alanı A nın, o hacmini çevreleyen herhangi kapalı bir yüzey üzerindeki yüzey integraline eşit olduğunu söyleyen ve gauss teoremi veya ıraksama teoremi olarak da bilinen matematiksel eşitliktir.