Merhaba arkadaşlar bu yazımızda compton olayı, compton saçılması ve compton saçılması formüllerini size konu anlatımı yapacağım. 1919 da Einstein E enerjili bir fotonun tek bir doğrultuda (bir küresel dalga gibi değil ) hareket ettiği ve E/c = hf/c kadar momentum taşıdığı sonucuna vardı. Kendi deyimiyle, “Bir ışıma demeti, bir molekülün hf enerji paketi kadar yayınlama veya yutma yapmasına yol açarsa, yutmak için gelen demede aynı yönde, yayınlama için demetle zıt yönde moleküle hf/c kadar momentum aktarılır.” 1923’te Arthur Holly Compton (1892-1962) ve Peter Debye (1884-1966) birbirlerinden bağımsız olarak Einstein’ın foton momentumu fikrini daha ileri götürdüler.
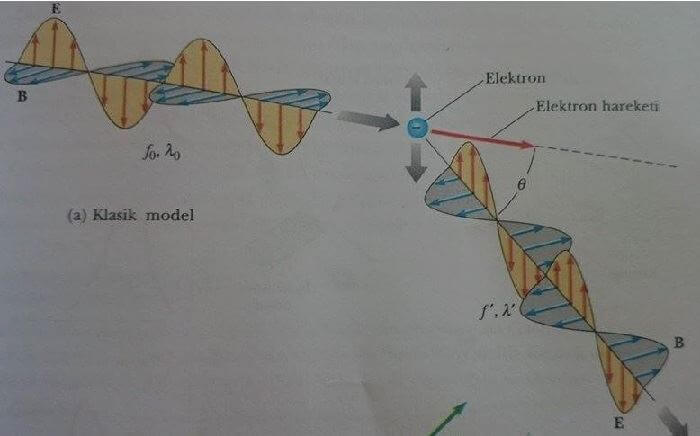
1922 yılında önce Compton ve çalışma arkadaşları x-ışınlarının elektronlardan saçılmasını klasik dalga teorisi ile açıklamanın mümkün olmadığını gösteren deliller topladılar. Klasik teoriye göre f0 frekanslı elektromanyetik dalgalar elektronlar üzerine düştüğünde, Şekli 1a da gösterilen iki etkiyi oluştururlar:
- (1) Işıma (radyasyon) basıncı elektronların dalganın ilerleme doğrultusunda ivmelenmelerine neden olur.
- (2) gelen ışımanın titreşen elektrik akımı, elektronları görünen frekans f ile titreştirmelidir, burada f’ hareketli elektronların referans sistemindeki frekanstır.
Bu görünen f’ frekansı Doppler etkisi nedeniyle gelen ışımanın f0 frekansından farklıdır. Her bir elektron enerji yutma işlemini hareketli parçacık olarak yapar ve ardından yine hareketli parçacık olarak ışıma yapar, böylece ışıma frekansında iki Doppler kayması oluşur.
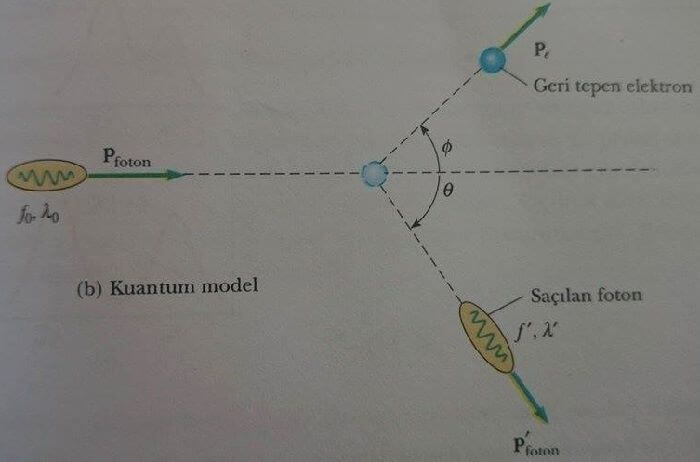
Elektromanyetik dalgalardan aldıkları enerji miktarına bağlı olarak farklı elektronlar etkileşmeden sonra farklı hızlarla hareket edeceklerinden, belirli bir açıya saçılmış dalganın frekansı, Doppler kaymalı değerler dağılımına sahip olmalıdır. Bu öngörü ile çelişen, Compton’un deneyleri verilen bir açıda yalnızca tek ışıma frekansı gözlendiğini gösterdi. Compton ve arkadaşları bu deneyleri, fotonları dalga olarak değil de hf enerjili ve hf/c momentumlu nokta parçacıklar olarak düşünerek ve her bir foton-elektron çarpışmasında enerji ve momentumun korunduğunu varsayarak açıklayabileceklerini anladılar. Compton, dalga yapısında olduğu çok iyi bilinen bir şey için bir parçacık modeli benimsiyordu ve bugün bu görüngü (fenomen) Compton olayı olarak bilinir. Şekil 1b de tek bir x-ışını fotonu ile bir elektron arasında momentum ve enerji değiş tokuşunun kuantum resmi görülmektedir.
Klasik ve kuantum modelleri arasındaki ikinci fark da Şekli 1b de gösterilmiştir. Klasik modelde elektron, ışıma basıncı tarafından gelen x-ışınının yayılma doğrultusunda itilir. Kuantum modelinde elektron, bilardo toplarının çarpışmasında olduğu gibi gelen ışıma doğrultusu ile Φ açısı yaparak saçılır.
Compton Olayı ve Saçılması
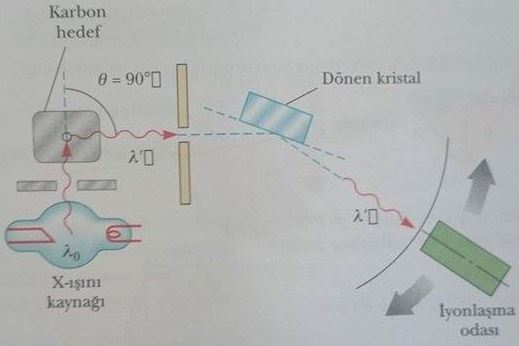
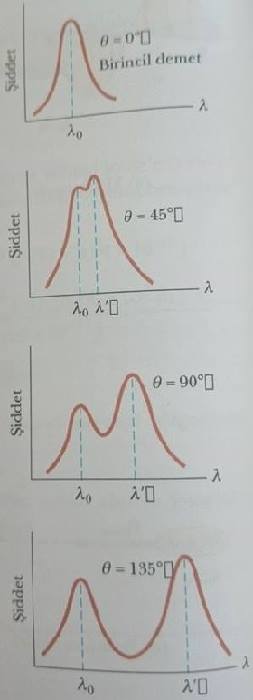
Şekil 1a Compton’un kullandığı düzeneğin şematik bir çizimidir. Grafit hedeften saçılan x-ışınları dönen kristal spektrometre ile analiz edilmiştir ve şiddet, şiddetle orantılı akım oluşturan bir iyonlaşma odası ile ölçülmüştür. Gelen demet dalga boyu λ0= 0,071 nm olan tek renkli x-ışınlarından oluşmuştur. Compton tarafından dört saçılma açısı (Şekil 2 daki θ açısı) için gözlenen deneysel dalga boyu-şiddet grafikleri Şekil 1b de gösterilmiştir. Sıfırdan farklı θ açıları için grafikler, biri λ0 da diğeri ise λ’ > λ0 da iki tepeye sahiptirler. λ’ deki kaymış tepe, serbest elektronlardan saçılan x-ışınlan tarafından oluştururulur. Compton, λ’ nün saçılma açısına bağlılığını
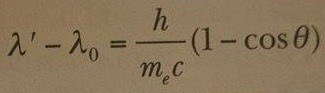
olarak öngörmüştür. Burada me,elektronun kütlesidir. Bu ifade Compton kayma eşitliği olarak bilinir ve h/me çarpanına elektronunu Compton dalga boyu (λc) adı verilir. Compton dalga boyunun günümüzde kabul edilen değeri
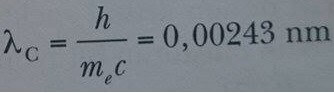
kadardır.
Şekil 3 deki λo değerinde oluşan kaymamış tepe, x-ışınlarının hedef atomlara sıkıca bağlı elektronlarından olan saçılmaları sonucu oluşur. Bu kaymamış tepenin varlığı, Eş. 2 de elektron kütlesi yerine, elektron kütlesinin yaklaşık 23 000 katı olan karbon atomu kütlesi konularak öngörülebilir. O halde, atoma bağlı bir elektrondan saçılmada dalga boyu kayması oluşur, ancak bu kanuna, Compton’un deneyinde algılanamayacak kadar küçüktür.
Compton’un ölçümleri Eş. 2 un öngörüleri ile çok iyi uyuşuyordu. Bu sonuçların gerçekten, pek çok fizikçiyi kuantum teorisinin kökten geçerli olduğuna inandıran ilk deliller olduğunu söylemek haksızlık olmaz. Compton olayını sizlere anlattım. Diğer yazımızda görüşmek üzere.

