Clapeyron Denklemi

Maxwell bağıntılarının termodinamikteki önemi göründüğünden daha büyüktür. Bu bağıntılar, termodinamik hesaplarda kullanılan başka bağıntıların çıkarılması için de temel oluştururlar. Clapeyron denklemi bu bağıntılardan biridir ve faz değişimiyle ilişkili entalpi değişimini, örneğin buharlaşma entalpisi h_fg‘yi, sadece P, v ve T değerlerinden yararlanarak hesaplamaya yardımcı olur.

Üçüncü Maxwell bağıntısı göz önüne alınarak aşağıdaki denklem elde edilir:

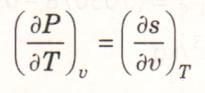
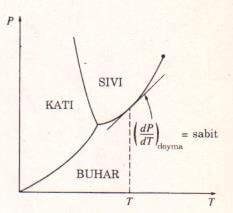
Faz değişimi sırasında basınç, sadece sıcaklığa bağlı olan doyma basıncıdır, bu nedenle özgül hacimden bağımsızdır. Başka bir anlatımla: F_doyma = f(T_doyma). Bu nedenle kısmi türev (dP/dT)_v, adi türev (dP/dT)_doyma olarak yazılabilir. (dP/dT)_doyma, P-T diyagramında doyma eğrisinin verilen bir doyma halindeki eğimidir (Şekil 1). Bu eğim özgül hacimden bağımsızdır, bu nedenle üstteki denklem, sabit sıcaklıkta, doymuş sıvı doymuş buhar halleri arasında integre edilirken sabit kalır. Örneğin, sıvının buhara dönüştüğü sabit sıcaklıktaki hal değişimi sırasında integrasyon aşağıdaki sonuçları verir.

Bu hal değişimi sırasında basınç da sabittir. Bu nedenle Maxwell bağıntıları sayesinde aşağıdaki denklem elde edilir.

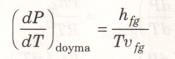
Bu denklem 1799-1864 yılları arasında yaşayan Fransız mühendis ve fizikçi E. Clapeyron’un adıyla, Clapeyron denklemi diye bilinir. Bu bağıntı önemli bir bağıntıdır, çünkü verilen bir sıcaklıkta, P-T diyagramında doyma eğrisinin eğimiyle doymuş sıvı ve doymuş buharın özgül hacimleri biliniyorsa, buharlaşma entalpisinin hesaplanmasına olanak sağlar.

Clapeyron denklemi sabit sıcaklık ve basınçta gerçekleşen herhangi bir faz değişimi için geçerlidir. Bu denklem genel olarak aşağıdaki şeklinde yazılabilir. Burada 1 ve 2 indisleri iki fazı göstermektedir.

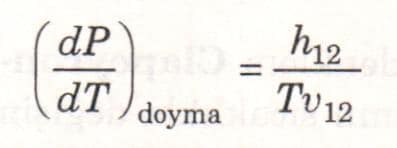
Clapeyron denklemi, sıvı buhar ve katı buhar faz değişimleri için, bazı yaklaşık işlemlerle, sadeleştirilebilir. Düşük basınçlarda, v_g » v_f olduğu için V_fg≅ v_g olur. Buhar mükemmel gaz kabul edilirse, v_g = RT/P yazılabilir. Bu değerler Clapeyron denklemin yerlerine konursa aşağıdaki ifade elde edilir.

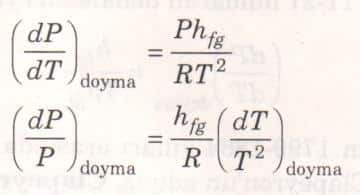
Küçük sıcaklık aralıklarında h_fg için ortalama sabit bir değer alınabilir. Böylece yukarıdaki denklem iki doyma hali arasında integre edilirse aşağıdaki bağıntı bulunur.

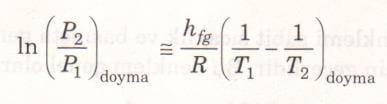
Yukarıdaki denklem Clapeyron-Clausius denklemi diye bilinir ve doyma basıncının sıcaklıkla değişimini gösterir. Bu denklem, buharlaşma entalpisi (h_fg) yerine sublimasyon entalpisini (h_ig) yazarak, katı buhar bölgesi için de kullanılabilir.