Friz dediğimiz yapılar Sym(X) yapılarını içeren X kümelerinin oluşturduğu ve geçişme özelliğini sağlayan “T” bir yapıdır. Daha düzgün bir söyleyişle belli bir kurala göre dize gelen düzgün doğrusal tek bir yöndeki sezgisel kümeler toplamıdır.
Yukarıda söz ettiğimiz tanımda “Sym(X)” X kümelerinin simetrilerinin oluşturduğu kümelerin hepsine verdiğimiz bir notasyon olup bu kümede açıkta kalan X’e bağlı hiçbir simetrik friz yoktur. Şayet iki desen (pattern) simetrik grup ise çok bariz olarak bu çift izomorfik yapılardır ki bu yapı izometriler içerir. (Örnek: Yansıma, döndürme…). Her friz ya da cebirsel şekillerin en az 7 desen kuralından birisine uymak zorundadır. Örneğin;
..FFFFFFFFFFFFFFFFFF..
Yukarıdaki harf sinsilesi simetri içermiyor dikkat edin biz buna tek bir yönde geçişme simetrileri demekteyiz. Matematiksel olarak bu simetri grubu sonsuz bir grup C∞ =〈T, I 〉olarak göstereceğiz ki öyle T’ler var ki sağdan bir birim yansımalıdır yani T(x,y) = (x+1,y).
..EEEEEEEEEEEEEEEE..
Bu desen ise paralel eksenlerin ayna simetrisi olarak adlandırılır. Bu simetri grubu ise C∞ × C2 =〈T, X | X2 = I, XT = TX〉olarak göstereceğiz. Bu noktada okurun gösterimleri anlamaya çalışmasını şiddetle tavsiye ediyoruz. X-eksenine göre yansıma olduğu için ve X(x, y) = (x, -y) için XT = TX eşitliği çok bariz. (Dikkat! x ve X’ler matematiksel olarak farklılık göstermektedir).
..AAAAAAAAAAAAAAA..
Bu desen yukarıda “E” desenine çok benzer ve aynadaki simetri düşümüdür. Geçişme simetrisi de diyebiliriz. Ama bu deseni farklı sadece bir tane değil sonsuz tane ayna simetri ekseni vardır. Simetri grubunu;
D∞ = 〈T, Y | Y2 = I, YT = T−1Y〉olarak gösterebiliriz.
T’yi yukarıda olduğu gibi bu sefer y-eksenine göre simetri olarak tanımladık ve eğer Y(x, y) = (-x, y) olduğunda YT = T-1Y eşitliğini gösterirsek işimiz daha açık ve net. Ayrıca biraz optikle ilgili olsa da, eğer ayna ekseni x=1/2 seçersek ve bu seçimi M ile tanımlarsak M(x, y) = (1-x, y) olur ve sadece T−1Y olur. Devam edelim…
…pbpbpbpbpbpbpbpb…
Bu sefer desende ayna simetrisi olmayıp düzgün simetri ekseni var yani belirli bir kural etrafında sonsuza uzanan anlamlı ya da anlamsız bloklar sinsilesi. Bu kuralı tanımlayacağız fakat desen iki farklı bileşke olarak görülebilir. pb frizi mi yoksa bp mi? Bu sorunun yanıtını sonsuz grup tanımıyla verelim. C∞ = 〈G | 〉 gösterimi bu desen için uygun olacaktır ki buradaki G’leri de G(x, y) = (x + 1⁄2 , y) tanımlamak mümkündür.
..NNNNNNNNNNNNNN..
Bu desen ise ne ayna simetrisi veya düzgün simetri ekseni içerir. Ama şanstan elimizde bu deseni tanımlayacağımız bir döndürme simetrisi vardır. Her N harfinin merkezleri bir döndürme simetrisi içindedir. Şayet bir tanesini ele alıp incelersek yani bir N harfinin merkezini alıp belli bir açıyla döndürüp belli bir müddet öteleme yaparsak istediğimiz deseni elde ederiz. Matematiksel olarak yine sonsuz bir grup olup gösterimi
D∞ = 〈T, R | R2 = I, RT = T−1R〉 şeklindedir.
Buradaki R ve T’leri ise döndürmelerin bir tanesine R dedik, R’lerin oluşturduğu geçişmeleri de T olarak tanımladık.
…HHHHHHHHHHHHHH..
H harflerinin oluşturduğu sonsuza giden bir desen. Bu desen çok şanslı. Nedeni ise 2 yönde hem döndürme hem de ayna simetrisine sahip. Bu deseni bir matematiksel simetri grubu olarak tanımlarsak bu grup düzgün bir gruptur. Bu simetri grubu geçişme, T ve 180°’lik merkezi döndürme biçimlerine sahiptir. Aslında matematiksel olarak;
D∞ × C2 = 〈T, M, R | M2 = R2 = 1, MT = TM, RM = MR, RT = T−1R〉olarak tanımlayabiliriz.
Yukarıda anlatmak istediğimiz her şeyi hatta daha fazlasını bu şekilde anlattık ki burada M’ler yansımalar, R’ler döndürmeler ve T’ler ise tüm geçişmelerin oluşturduğu parça olarak tanımlayabiliriz.
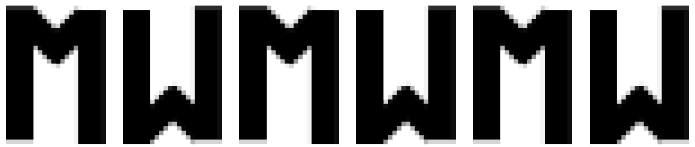 Yukarıdaki şekil ise sonsuza gittiğini düşünelim. Ne derseniz? Bir ters bir düz M harfinin oluşturduğu desenler ne anlam ifade etmektedir. Bu desen ardışık iki harfin merkezleri arasında döndürme simetrisi ayrıca yatay doğrular boyunca her harfin tam orta noktasında ayna simetrini elde ederiz. Başımız hemen sıkıştığı için matematiksel bir tanımlara yer verelim.
Yukarıdaki şekil ise sonsuza gittiğini düşünelim. Ne derseniz? Bir ters bir düz M harfinin oluşturduğu desenler ne anlam ifade etmektedir. Bu desen ardışık iki harfin merkezleri arasında döndürme simetrisi ayrıca yatay doğrular boyunca her harfin tam orta noktasında ayna simetrini elde ederiz. Başımız hemen sıkıştığı için matematiksel bir tanımlara yer verelim.
G(x, y) = (x + 1⁄2 , −y) ve T(x, y) = (x + 1, y)’ lerin oluşturduğu parçalardır ki iki eşitlikten G2 = T çok bariz! Şayet 180°’lik bir döndürme simetrisi uygularsak bu son oluşan döndürmeyi R(x, y) = (-x, -y) ile gösterebiliriz ve x=1/4 ekseninin yansıma simetrilerini M(x, y) = (1⁄2 – x, y) olarak tanımlayabiliriz. Aynı şekilde RM = G okur tarafından çok kolay şekilde açığa çıkarılabilir.
〈R, M | R2 = M2 = 1〉 bu tanım yukarıda verdiğimiz G(x,y) ve T(x,y) lerin ortak gösterimi diyebiliriz. Bu desen için aslında bu tanım daha uygun olur. Ama şu bir gerçek ki R ile M arasında hiçbir ilişki bulamayız. Ama
S = RM gibi bir ifade seçersek D∞=〈S, R | R2 = 1, RS = S−1R〉 olur. Yukarıda anlattığımız bilgi topluluğunu bir teoremle açıklayalım.
Teorem: Tüm friz desenleri yukarıda saydığımız kurallardan en az birisine uymak zorundadır.
Kanıt: Diyelim X friz deseni olsun ve içinde Sym(X) ve yatay eksenler boyunca geçişme sağlayan T’yi içersin. Şimdi tanımlamamız gereken simetri biçimlerini açıklayalım.
V: Yatay eksenlerde dikey yansımalar
H: Yatay eksenlerdeki yansımlar
R: Döndürmeler – Rotasyonlar
G: Düzgün yatay yansımalar
Toplam en fazla 24 = 16 tane friz desen çeşidi vardır.
H ⇒ G: Eğer Sym(X) yatay eksenlerde yansıma içeriyorsa bunun sonucunda düzgün simetrilerde içerir.
RG ⇒ H: İki döndürme bileşkesinin çarpımı bütün düzgün yatay yansımalarda belirgindir ve bu durum dikey eksende yatay yansıma olmak zorundadır.
GV ⇒ R: Düzgün yatay yansımalar ve dikey yansımaların çarpımı bir noktada belirgindir. Bu isometriler döndürme olmak zorundadır.
RV ⇒ G: Döndürme ve yatay yansımaların çarpımı sadece yatay bir doğrudur. Bu yüzden ya yatay yansıma ya da yatay glide’tır. Kısacası Sym(X) glide içerir.
Dediğimiz gibi her şekil friz olmayabilir. Friz olabilmenin şartı yukarıda saydığımız kombinasyonları sağlamasıdır. Bu yazıyı en iyi anlatacak çok sade bir tablo oluşturacağız. Tabloyu anlayan okur vereceğimiz örnekleri çözmesinde bir mahsur görmemekteyiz.
Kombinasyon |
Desen Çeşitleri |
| Hiçbiri | F |
| V | A |
| R | N |
| G | pb |
| HG | E |
| VG | MW |
| VRGH | H |
Örnekler: Aşağıdaki friz örneklerini inceleyelim.
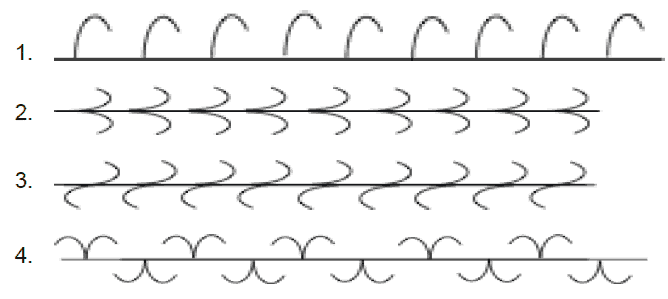 5. Sinx, cosx, tanx, cotanx, fonksiyonlarının grafikleri hangi friz desenlerine denk gelmektedir.
5. Sinx, cosx, tanx, cotanx, fonksiyonlarının grafikleri hangi friz desenlerine denk gelmektedir.
Kaynak
- Duane M.Broline, D.W.Crowe & I.M. Isaacs, The goemetry of frieze pattern Geometriae Dedicate, 3(1974)

