Çarpışmalar Konu Anlatımı

Merhaba arkadaşlar bu yazımızda sizlere bir boyutta esnek olmayan çarpışmalar, tamamen esnek olmayan çarpışmalar, esnek çarpışmalar ve iki boyutta çarpışmaları anlatacağım. Bu kesimde, iki parçacık birbiriyle çarpışınca ne olacağını anlamak için mo­mentum korunumu yasasını kullanacağız. Çarpışma terimini, iki parçacığın birbiri üzerine impulsif kuvvetler oluşturarak kısa bir süre için birlikte olmala­rı şeklinde tanımlayacağız. Çarpışmadaki itme (impulsif) kuvvetinin, mevcut dış kuvvetlerden daha büyük olduğu kabul edilecektir.

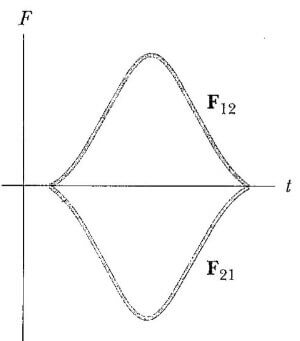
Çarpışma, iki cisim arasındaki fiziki temasın sonucu olabilir. Ancak çarpışma kelimesiyle söylenmek istenen, genelleştirilmelidir çünkü mikroskopik ölçeğe dayalı “fiziki temas” yanlış bir tanımdır ve anlamsızdır. Bunu anlamak için atomik ölçekte bir çarpışma göz önüne alalım: bir protonun bir alfa parçacığı (Helyum atomunun çekirdeği) ile çarpışması gibi. Parçacıklar pozitif yüklü olduklarından asla birbirleriyle fiziki temasta bulunamazlar; aralarındaki kuvvetli elektrostatik itmeden dolayı bir­birlerinden biraz uzaktırlar. m₁ ve m₂ kütleli iki parçacık çarpıştığı zaman, impulsif kuvvetler (itme kuvvetleri) Şekil 2’de görüldüğü gibi karmaşık bir şekilde zamanla değişebilir. Eğer F₂₁, m₂’nin m₁ üzerine uygula­dığı kuvvetse, parçacıklar üzerine hiçbir dış kuvvetin etkimeyeceğini göz önü­ne alırsak, çarpışmadan dolayı m₁’in momentumundaki değişme

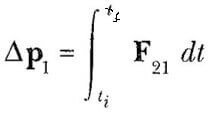
olarak yazılabilir. Benzer şekilde, m₁’in m₂ üzerine uyguladığı kuvvet F₁₂ olmak üzere, m₂’nin momentumundaki değişim de

formül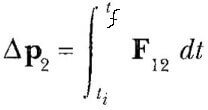

ile verilir. Nitekim Newton’un üçüncü yasasına göre şu sonucu yazabiliriz:

Δp₁ = – Δp₂

Δp₁ + Δp₂ = 0

Sistemin toplam momentumu p_sistem = p₁ + p₂ olduğundan, çarpışmadan do­layı sistemin momentumundaki değişimin sıfır olduğu sonucuna varırız. Bu da,

p_sistem = p₁ + p₂ = sabit

demektir. Sisteme hiçbir dış kuvvet etki etmediğinden bu sonuç tam olarak beklediğimiz sonuçtur. İtme kuvvetleri iç kuvvetler olduğundan, sistemin momentumunu değiştiremezler (sadece dış kuvvetler değiştirir). Buradan şu sonucu çıkarırız: Yalıtılmış bir sistemin çarpışmadan hemen önceki toplam momentumu, çarpışmadan hemen sonraki toplam momentumum eşit­tir.

Bir Boyutta Esnek Olmayan Çarpışmalar

Dış kuvvetlerin dikkate alınmadığı bir çarpışmada momentumun korunduğu­nu gördük. Fakat çarpışmanın türüne bağlı olarak kinetik enerji sabit kalma­yabilir. Gerçekte, kinetik enerjinin çarpışmadan önce ve sonra aynı olup olma­ması, çarpışmanın esnek veya esnek olmadığını belirlemede kullanılır.

İki cismin arasındaki esnek çarpışma, toplam momentum ve toplam kinetik enerjinin çarpışmadan önce ve sonra sabit kaldığı çarpışmadır. Bilardo topu çarpış­maları ve herhangi bir sıcaklıkta hava moleküllerinin duvarla çarpışması yak­laşık olarak esnektir. Gerçek esnek çarpışmalar, atom ve atom altı parçacıklar arasında gerçekleşir. Makroskobik dünyada bilardo toplan gibi belirli cisimler arasındaki çarpışmalar yaklaşık olarak esnektir, çünkü bazı bozulmalar ve ki­netik enerji kaybı oluşur.

Bir esnek olmayan (in elastik) çarpışma, momentum korunduğu halde toplam kinetik enerjinin çarpışmadan önce ve sonra aynı olmadığı çarpışmadır. Esnek olma­yan çarpışmalar iki çeşittir. Bir meteor taşının yere çarpışında olduğu gibi, çar­pışan cisimlerin çarpışmadan sonra birlikte hareket ettiği çarpışma, tamamen esnek olmayan çarpışma olarak adlandırılır. Bir lastik topun katı bir yüzeyle çarpışması, gibi çarpışan cisim diğerine yapışıp kalmıyor ama biraz kinetik enerji kaybediyorsa çarpışma esnek olmayan çarpışmadır. Örneğin lastik top katı yüzeyle çarpıştığında, çarpışma in elastiktir çünkü top şekil değiştirmiş ve kinetik enerji kaybetmiştir.

Pek çok çarpışmada, kinetik enerji çarpışmadan önce ve sonra aynı değil­dir, çünkü cismin şekli bozulduğunda, bu enerjinin bir kısmı iç enerjiye, es­neklik potansiyel enerjisine ve dönme enerjisine dönüşür. Esnek ve tamamen esnek olmayan çarpışmalar sınır halleridir; pek çok çarpışma, bu ikisi arasında oluşur.

Bu kesimin kalan kısmında, bir-boyuttaki çarpışmaları ve iki sınır durumu­nu esnek ve tamamen esnek olmayan çarpışmaları göz önüne alacağız. Bu iki tür arasındaki önemli farklılık şu şekilde ifade edilir: Bütün çarpışmalarda mo­mentum sabittir fakat kinetik enerji sadece esnek çarpışmalarda sabit kalır.

Tamamen Esnek Olmayan Çarpışmalar

Doğrusal bir yol boyunca ilk v_1i ve v_2i hızları ile hareket eden m₁ ve m₂ kütleli iki parçacığı ele alalım. Çarpışmadan sonra iki cisim bir­birine yapışır ve v_s ortak hızı ile hareket ederse, sistemin sadece momentumu korunur. Bu nedenle, çarpışmadan önceki toplam momentumun, çarpışma­dan sonraki birleşik sistemin toplam momentumuna eşit olduğunu söyleyebi­liriz. Yani,

m₁ v_1i + m₂ v_2i = (m₁ + m₂)v_f (eşitlik 1)

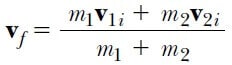
olur.

Esnek Çarpışmalar

Şimdi, kafa-kafaya esnek çarpışmaya uğrayan iki parçacığı ele alalım (Şekil 3). Bu durumda momentum ve kinetik enerji birlikte korunur; bu neden­le şu eşitlikleri yazabiliriz:

m₁ v_1i + m₂ v_2i = m₁v_1f + m₂v_2f (eşitlik 3)

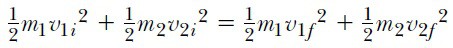
Şekil 3’daki hızların tümü ya sağa ya da sola yönelik okluğundan, yönleri­ni gösteren cebirsel işaretleri ile birlikte süratleri cinsinden temsil edilebilir. Burada, parçacık sağa ilerlerken v pozitif, sola ilerlerken negatiftir. Bilindiği gibi, v ye “sürat” demek uygun olur; yani cebirsel bir işa­reti olmayan hız vektörünün büyüklüğüdür.

Esnek çarpışmalarla ilgili herhangi bir problemde iki tane bilinmeyen var­dır; eşitlik 3 ve eşitlik 4, bunları bulmak için birlikte çözülür. Alternatif bir yaklaşım, 4 Eşitliğini farklı bir şekilde yazmaktır; bu da matematik işlemi basitleştirir. Buna göre, 4 Eşitliğinde 1/2 katsayısı kaldırılıp ifade yeniden yazılınca

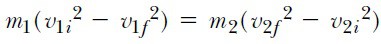
olur. Şimdi eşitliğin iki tarafı çarpanlara ayırılırsa,

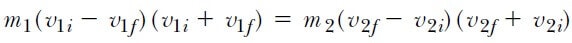
olur. Şimdi, (eşitlik 3) Eşitliğini, m₁ ve m₂’yi ayrı ayrı ihtiva edecek şekilde

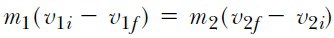
olarak yazabiliriz. 5 Eşitliğini, 6 Eşitliğine bölerek

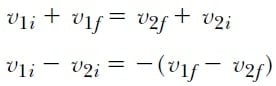
şeklinde eşitliği elde edilir.

Bu eşitlik,eşitlik 3 ile birlikte esnek çarpışma ile ilgili problemleri çözmek için kullanılabilir. 7 Eşitliğine göre iki cismin çarpışma öncesi bağıl hızları (v_1i – v_2i), çarpışma sonrası bağıl hızlarının negatifine, -( v_1f — v_2f), eşittir.

Parçacıkların kütleleri ve ilk hızlarının bilinmesi halinde, iki eşitlik ve iki bilinmeyen olduğundan, eşitlik 3 ve eşitlik 7 ilk hızlar cinsinden son hızla­rın bulunmasına olanak verir. Böylece v_1f ve v_2f şunlar olur:

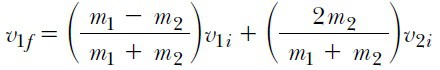
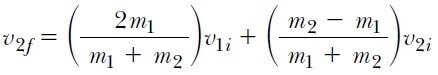
v_1i ve v_2i hızları vektörel nicelikler olduğundan, 8 ve 9 eşitliklerinde bunların işaretleri de konmalıdır. Örneğin başlangıçta m₂ sola hareket ediyor­sa, v_2i negatif alınır.

Şimdi bazı özel durumları inceleyelim: Kütleler eşitse (m₁ = m₂), v_1f = v_2i ve v_2f = v_1i olur. Yani, parçacıkların hızları değiş-tokuş olmuştur. Bu da bilar­do toplarında gözlediğimiz durumdur. Çarpılan top, çarpan topun hızı ile ha­reket eder.

İkinci kütle başlangıçta durgun ise, v₂i = 0, 8 ve 9 Eşitlikleri aşağıda­ki şekli alır:

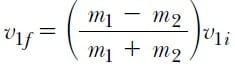
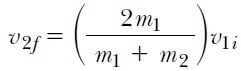
m₁’in m₂’den çok büyük olması halinde, 10 ve 11 Eşitliklerinden v_1f ≈ v_1i ve v_2f ≈ 2v_1i olduğunu görürüz. Yani ağır bir parçacık, durmakta olan hafif bir parçacıkla çarpışınca, ağır parçacık kendi ilk hızı ile hareket ederken, başlangıçta durgun olan hafif parçacık, diğerinin ilk hızının iki katına eşit bir hız­la hareket eder. Böyle bir çarpışma örneği, uranyum gibi hareketli ağır bir atomla hidrojen gibi durgun hafif bir atomun çarpışmasıdır.

m₂ kütlesi m₁’den çok büyük ve başlangıçta durgun ise, v_1f ≈ -v_1i ve v_2f ≈ v_2i = 0 olduğu görülür. Yani, çok hafif bir parçacık, durgun olan çok ağır bir parçacıkla çarpışınca, ağır parçacık yaklaşık olarak sükûnetini korurken, hafif parçacık aynı hızla yön değiştirir.

İki Boyutta Çarpışmalar

Yalıtılmış iki parçacıklı bir sistemin toplam momentumunun korunduğu gösterildi. Bu sonuç, iki parçacığın herhangi bir çarpışması için de x,y ve z doğrultularının her birinde toplam momentumun korunacağı­nı ortaya koyar. Ancak çarpışmaların önemli bir bölümü düzlemde yer alır. Bi­lardo oyunu iki-boyutlu bir yüzey üzerinde hareket eden cisimlerin çoklu çar­pışmalarına bir örnektir. İki-boyutlu çarpışmalar için momentum korunumuyla ilgili iki bileşenli eşitlik elde ederiz:

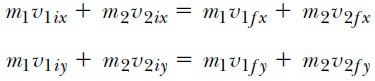
Başlangıçta durgun olan m₂ kütleli bir parçacıkla, m₁ kütleli bir parçacığın iki boyutta çarpışmasını ele alalım (Şekil 4). Çarpışmadan sonra m₁ kütlesi yatayla θ ve m₂ kütlesi Φ açısı ile hareket eder. Bu durum sıyırmalı çarpışma ola­rak adlandırılır.

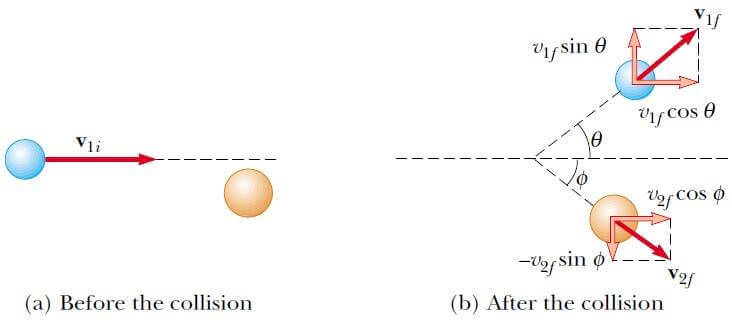
Momentumun korunumu kanununu, her iki parçacığın momentumlarının başlangıçtaki y bileşenlerinin sıfır olduklarına dikkat ederek şöyle yazabiliriz:

m₁v_1i = m₁v_1f cosθ + m₂v_2f cosΦ(eşitlik 12)

0 = m₁v_1f sinθ – m₂v_2f sinΦ (eşitlik 13)

13 Eşitliğindeki negatif işaret, çarpışmadan sonra ikinci parçacığın hızının y bileşeninin aşağı yönlü olması gerçeğinden ileri gelir. Şimdi iki bağımsız eşit­liğe sahibiz. 12 ve 13 Eşitliklerindeki yedi nicelikten sadece ikisi bilinmiyor­sa problem çözülebilir.

Çarpışma esnekse 4 Eşitliğini (kinetik enerji korunumu) kullanabiliriz. v_2i = 0 alınarak

½ m₁v_1i² = ½ m₁v_1f² + ½ m₂v_1f² (eşitlik 14)

yazılabilir. Eğer ilk hız v_1i ve kütleler bilinirse geriye dört bilinmeyen (v_1f, v_2f, θ, Φ) kalır. Elimizde üç eşitlik bulunduğundan, sadece korunum kanunlarına göre çarpışmadan sonraki hareketi çözümlemek için, diğer dört nicelikten (v_1f, v_2f, θ, Φ)birinin daha verilmesi gerekir.

Yine, çarpışmanın esnek olmaması halinde, kinetik enerjinin korunmadığı­na ve 14 Eşitliğinin uygulanamayacağına dikkat etmek gerekir.

Çarpışmalar

İki cisim arasındaki çarpışmalarla ilgili problemleri çözmek gerektiğinde şu işlemler tavsiye edilir:

• Bir koordinat sistemi oluşturunuz ve hızları bu sistem üzerinde gösteri­niz. İlk hızlardan birini x-ekseni üzerine almak en uygun olanıdır.
• Koordinat sisteminde, bütün hız vektörlerini çiziniz ve değerlerini üze­rinde gösteriniz.
• Çarpışmadan önce ve sonra her cismin momentumunun x ve y bileşen­leri için eşitlikleri yazınız. Hız vektörlerinin bileşenleri için uygun işaret­leri belirtiniz. Mesela, bir cismin negatif x yönünde hareket etmesi halin­de hızının x bileşeni negatif alınmalıdır. İşaret belirlemede dikkatli ol­mak esastır.
• Çarpışmadan önce ve sonra, x doğrultusundaki toplam momentum ifa­delerini yazıp birbirine eşitleyiniz, bu işlemi y doğrultusu için de yapınız. “İfadeleriniz, herhangi bir çarpışmada sistemin momentumu koruduğun­dan, herhangi bir doğrultudaki toplam momentum da korunmalıdır” gerçeğine dayanır. Burada korunan ayrı ayrı parçacıkların momentumları olmayıp, sistemin momentumu olduğuna dikkat etmek gerekir.
• Esnek olmayan çarpışmada kinetik enerji korunmaz ve bilinmeyen nice­likler için momentum eşitliklerini çözmemiz gerekir.
• Esnek çarpışmada kinetik enerji de korunur. Yani, çarpışmadan önce ve sonraki toplam kinetik enerjileri de eşitleyebilirsiniz. Bu da çeşitli hızlar arasında ilave bir bağıntı verir.