Sevgili matematik meraklıları, bugün sizlerle matematiğin belki de en temel ve bir o kadar da heyecan verici konularından biri olan “Bölme ve Bölünebilme” hakkında konuşacağız. Evet, doğru duydunuz, heyecan verici! Çünkü bu konu, günlük hayatımızda farkında olmadan sık sık kullandığımız ve aslında matematiğin büyülü dünyasına açılan kapılardan biri.
Bölme İşlemi Nedir?
Hadi gelin, önce en temel soruyla başlayalım: Bölme nedir? Basitçe ifade etmek gerekirse, bölme, bir sayıyı eşit parçalara ayırma işlemidir. Düşünsenize, bir pizzayı arkadaşlarınızla paylaşırken aslında bir bölme işlemi yapıyorsunuz!
Bölme İşleminin Temel Kavramları
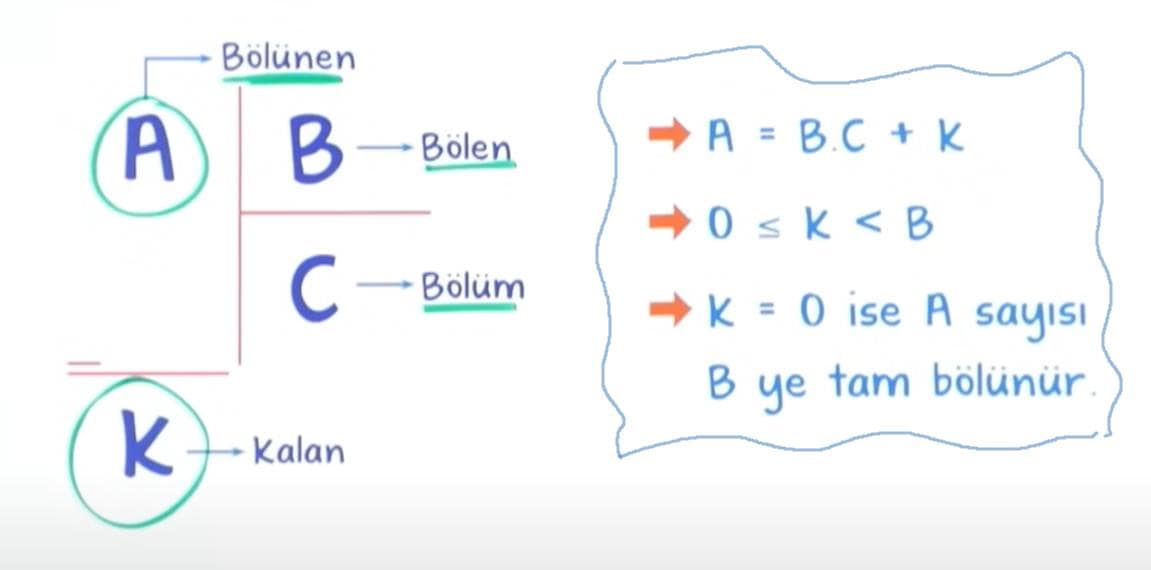
Bölme işleminde karşımıza çıkan bazı terimler var. Bunları bir ailenin üyeleri gibi düşünebiliriz:
- Bölünen: Paylaşılacak olan miktar. Yani pizzamız!
- Bölen: Kaç kişiye paylaştıracağımız. Aç arkadaşlarımızın sayısı!
- Bölüm: Her kişiye düşen miktar. Herkesin tabağındaki pizza dilimi!
- Kalan: Eşit olarak paylaştırılamayan kısım. Bazen son bir dilim kalır, değil mi?
Bölme İşleminin Günlük Hayattaki Önemi
“Peki ama neden öğreniyoruz bunu?” diye sorduğunuzu duyar gibiyim. Haklısınız, bu soruyu sormak çok doğal. Bölme işlemi, günlük hayatımızda sandığımızdan çok daha fazla yer alıyor. Örneğin:
- Alışverişte bütçemizi planlarken
- Yemek yaparken malzemeleri ölçerken
- Zamanımızı etkin bir şekilde yönetirken
Hep bölme işlemi yapıyoruz aslında. Yani bölme, sadece matematik dersinde karşımıza çıkan soyut bir kavram değil, hayatımızın her alanında kullandığımız pratik bir araç!
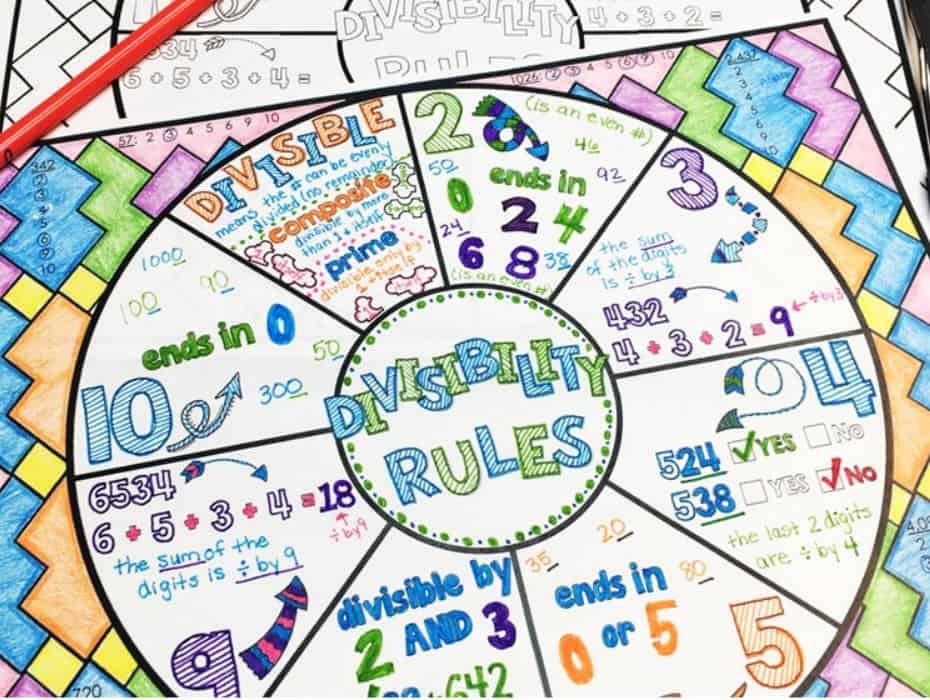
Bölünebilme Kuralları
Şimdi gelelim işin biraz daha eğlenceli kısmına: Bölünebilme kuralları! Bu kurallar, büyük sayılarla uğraşırken işimizi inanılmaz derecede kolaylaştıran sihirli formüller gibidir.
2 ile Bölünebilme
2 ile bölünebilme, belki de en kolay kuraldır. Bir sayının 2 ile bölünebilmesi için ne gerekir biliyor musunuz? Sadece son basamağının çift olması! Yani 0, 2, 4, 6 veya 8 ile bitmesi yeterli. Ne kadar kolay, değil mi?
Örnek: 1358 sayısı 2 ile bölünebilir mi? Evet, çünkü 8 ile bitiyor!
3 ile Bölünebilme
3 ile bölünebilme kuralı biraz daha ilginç. Bir sayının 3 ile bölünebilmesi için, rakamlarının toplamının 3’e bölünebilmesi gerekiyor.
Örnek: 453 sayısı 3 ile bölünebilir mi? Hadi hesaplayalım: 4+5+3=12. 12 de 3’e bölünebilir, o zaman 453 de 3’e bölünebilir!
4 ile Bölünebilme
4 ile bölünebilme kuralı, 2 ile bölünebilme kuralının biraz daha gelişmiş hali gibidir. Bir sayının 4 ile bölünebilmesi için, son iki basamağının oluşturduğu sayının 4’e bölünebilmesi gerekir.
Örnek: 1724 sayısı 4 ile bölünebilir mi? Son iki basamak 24, ve 24 4’e bölünebilir. O zaman 1724 de 4’e bölünebilir!
5 ile Bölünebilme
5 ile bölünebilme kuralı, 2 ile bölünebilme kadar kolaydır. Bir sayının 5 ile bölünebilmesi için son basamağının 0 veya 5 olması yeterlidir.
Örnek: 2735 sayısı 5 ile bölünebilir mi? Evet, çünkü 5 ile bitiyor!
6 ile Bölünebilme
6 ile bölünebilme kuralı, 2 ve 3 ile bölünebilme kurallarının bir kombinasyonudur. Bir sayının 6 ile bölünebilmesi için hem 2 hem de 3 ile bölünebilmesi gerekir.
Örnek: 1236 sayısı 6 ile bölünebilir mi? 2 ile bölünebilir çünkü çift sayı. 1+2+3+6=12, 12 de 3’e bölünebilir. O zaman 1236 sayısı 6 ile bölünebilir!
9 ile Bölünebilme
9 ile bölünebilme kuralı, 3 ile bölünebilme kuralına benzer. Bir sayının 9 ile bölünebilmesi için, rakamlarının toplamının 9’a bölünebilmesi gerekir.
Örnek: 4572 sayısı 9 ile bölünebilir mi? 4+5+7+2=18, 18 de 9’a bölünebilir. O zaman 4572 de 9’a bölünebilir!
10 ile Bölünebilme
10 ile bölünebilme kuralı belki de en kolayıdır. Bir sayının 10 ile bölünebilmesi için son basamağının 0 olması yeterlidir.
Örnek: 3450 sayısı 10 ile bölünebilir mi? Evet, çünkü 0 ile bitiyor!
Bölme ve Bölünebilme Soru ve Çözümü
Basit Soru: 2346 sayısı hangi sayılara tam olarak bölünebilir? (2, 3, 4, 5, 6, 9 seçeneklerini kontrol ediniz.)
Çözüm:
Hadi basamak basamak ilerleyelim:
- 2 ile bölünebilme: Son basamak çift sayı (6), o halde 2’ye bölünür.
- 3 ile bölünebilme: Rakamların toplamı 2+3+4+6 = 15. 15, 3’e bölünür, o halde sayı 3’e bölünür.
- 4 ile bölünebilme: Son iki basamak 46. 46, 4’e bölünür, o halde sayı 4’e bölünür.
- 5 ile bölünebilme: Son basamak 6, o halde 5’e bölünmez.
- 6 ile bölünebilme: Hem 2’ye hem 3’e bölündüğü için 6’ya da bölünür.
- 9 ile bölünebilme: Rakamların toplamı 15. 15, 9’a bölünmez, o halde sayı 9’a bölünmez.
Sonuç: 2346 sayısı 2, 3, 4 ve 6’ya tam olarak bölünebilir.
Zor Soru: A ve B iki farklı rakamı temsil etmektedir. AB5A8B şeklinde yazılan 6 basamaklı bir sayı 72’ye tam bölünmektedir. A’nın alabileceği en büyük değer kaçtır?
Çözüm:
Bu soruyu çözmek için adım adım ilerleyelim:
- Bir sayının 72’ye bölünebilmesi için hem 8’e hem de 9’a bölünebilmesi gerekir.
- 8’e bölünebilme kuralı: Son üç basamağın oluşturduğu sayının 8’e bölünebilmesi gerekir. Yani A8B, 8’e bölünmelidir.
- 9’a bölünebilme kuralı: Rakamların toplamının 9’a bölünebilmesi gerekir. Yani A+B+5+A+8+B = 2A+2B+13, 9’a bölünmelidir.
- A8B’nin 8’e bölünebilmesi için B çift sayı olmalıdır. En büyük çift sayı 8’dir, ama B ≠ 8 çünkü sayıda zaten 8 var. O halde B’nin alabileceği en büyük değer 6’dır.
- 2A+2B+13’ün 9’a bölünebilmesi için, 2A+2(6)+13 = 2A+25’in 9’a bölünebilmesi gerekir.
- 2A+25’in 9’a bölünebilmesi için A = 7 olmalıdır. Çünkü: 2(7)+25 = 39, ve 39 9’a bölünür.
- A8B’nin 8’e bölünebilmesi için: 786 sayısı 8’e bölünebilir mi? Evet.
Sonuç: A’nın alabileceği en büyük değer 7’dir.
Bu zor soru, bölünebilme kurallarının birlikte kullanılmasını ve sistematik düşünmeyi gerektiriyor. Aynı zamanda, problem çözme becerilerini de test ediyor.
Bölünebilme Kurallarının Pratik Uygulamaları
Peki, bu kuralları nerede kullanacağız? İşte size birkaç örnek:
- Alışverişte: İndirimli fiyatları hızlıca hesaplamak için (örneğin %10 indirim, 10’a bölünebilen fiyatlarda çok kolay hesaplanır)
- Zaman planlamasında: Bir işi eşit parçalara bölerken (örneğin 60 dakikalık bir süreyi 3’e bölmek)
- Oyunlarda: Puan hesaplamalarında veya grup oluştururken
Gördüğünüz gibi, bu kurallar hayatımızın her alanında işimize yarayabilir!
Asal Sayılar ve Bölünebilme
Şimdi biraz daha derine inelim ve asal sayılarla bölünebilme arasındaki ilişkiye bakalım. Asal sayılar, sadece 1’e ve kendisine bölünebilen sayılardır. 2, 3, 5, 7, 11 gibi.
Asal Çarpanlar ve Bölünebilme İlişkisi
Her sayı, asal çarpanlarına ayrılabilir. Örneğin:
12 = 2 x 2 x 3
Bu, 12’nin 2 ve 3 ile bölünebileceği anlamına gelir. Aynı zamanda 4 (2×2) ve 6 (2×3) ile de bölünebilir.
Bu bilgi, büyük sayılarla çalışırken çok işimize yarar. Örneğin, 360 sayısını düşünelim:
360 = 2^3 x 3^2 x 5
Bu, 360’ın 2, 3, 5, 4, 9, 10, 6, 18, 30, 36, 90 ve 180 ile bölünebileceği anlamına gelir. Ne kadar da çok böleni varmış, değil mi?
EBOB ve EKOK’un Bölünebilme ile İlişkisi
EBOB (En Büyük Ortak Bölen) ve EKOK (En Küçük Ortak Kat) kavramları da bölünebilme ile yakından ilişkilidir.
EBOB, iki veya daha fazla sayının ortak bölenlerinin en büyüğüdür. Örneğin, 12 ve 18’in EBOB’u 6’dır.
EKOK ise iki veya daha fazla sayının ortak katlarının en küçüğüdür. 12 ve 18’in EKOK’u 36’dır.
Bu kavramlar, günlük hayatta problem çözmede çok işimize yarar. Örneğin, farklı uzunluktaki iki ipi tam olarak kullanmak için kaç parçaya bölmemiz gerektiğini bulmak için EBOB’u kullanabiliriz.
Sonuç: Bölme ve Bölünebilmenin Önemi
İşte sevgili okurlar, bölme ve bölünebilme konusunda bilmeniz gereken temel bilgileri ele aldık. Gördüğünüz gibi, bu konu sadece matematik derslerinde karşımıza çıkan soyut bir kavram değil, hayatımızın her alanında kullandığımız pratik bir araç.
Bölme ve bölünebilme kurallarını anlamak, sadece matematik notlarınızı yükseltmekle kalmaz, aynı zamanda günlük hayatta karşılaştığınız problemleri çözme becerinizi de geliştirir. Alışverişte indirimli fiyatları hızlıca hesaplamaktan tutun, zamanınızı etkili bir şekilde planlamaya kadar pek çok konuda size yardımcı olur.
Unutmayın, matematik korkulacak bir canavar değil, aksine hayatı daha iyi anlamamıza ve yönetmemize yardımcı olan bir araçtır. Ve bölme ile bölünebilme, bu aracın en temel ve kullanışlı parçalarından biridir.
Sayıların büyülü dünyasında keyifli yolculuklar! Kim bilir, belki de bir gün siz de büyük matematiksel keşiflere imza atacaksınız. Sonuçta, her büyük keşif, küçük bölmelerle, ya da bizim durumumuzda, küçük bölünebilme kurallarıyla başlar!
Sıkça Sorulan Sorular (SSS)
- Soru: Bir sayının aynı anda hem 3 hem de 4 ile bölünebilmesi için hangi kurala uyması gerekir? Cevap: Bir sayının hem 3 hem de 4 ile bölünebilmesi için 12 ile bölünebilmesi gerekir. Bu durumda, sayının son iki basamağının 4’e bölünebilmesi ve aynı zamanda tüm rakamlarının toplamının 3’e bölünebilmesi gerekir.
- Soru: 7 ile bölünebilme kuralı nedir? Cevap: 7 ile bölünebilme kuralı biraz daha karmaşıktır. Sayının son basamağını 2 ile çarpıp, kalan basamaklardan çıkarırız. Elde edilen sonuç 7’ye bölünebiliyorsa, orijinal sayı da 7’ye bölünebilir. Bu işlemi elde edilen yeni sayı üzerinde tekrarlayabiliriz.
- Soru: Bölünebilme kurallarını öğrenmenin en etkili yolu nedir? Cevap: Bölünebilme kurallarını öğrenmenin en etkili yolu, düzenli pratik yapmak ve günlük hayatta uygulamaktır. Alışveriş yaparken fiyatları hızlıca bölmeye çalışmak, takvimde tarihleri bölünebilirlik açısından incelemek gibi günlük aktiviteler, bu kuralları pekiştirmenize yardımcı olacaktır. Ayrıca, her kuralı bir hikaye veya görsel bir imge ile ilişkilendirmek de hatırlamayı kolaylaştırabilir.
- Soru: Bir sayının 8 ile bölünebilme kuralı nedir ve neden bu kural işe yarar? Cevap: Bir sayının 8 ile bölünebilmesi için, son üç basamağının oluşturduğu sayının 8’e bölünebilmesi gerekir. Örneğin, 23.456 sayısı 8’e bölünebilir mi? Son üç basamak 456’dır ve 456 ÷ 8 = 57 olduğu için, 23.456 sayısı 8’e bölünebilir. Bu kural işe yarar çünkü 8 = 2^3 olduğundan, bir sayının 8’e bölünebilmesi için 2’ye üç kez bölünebilmesi gerekir. Son üç basamak bu bilgiyi bize verir.