Bir Yayın Yaptığı İş Nedir

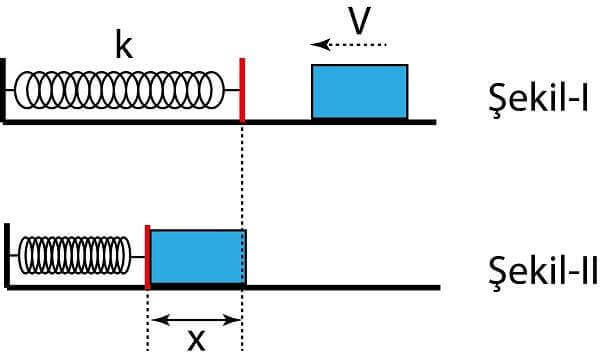
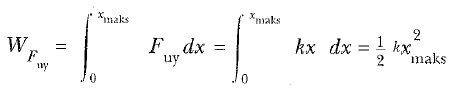Merhaba arkadaşlar bu yazımızda sizlere bir yayın yaptığı iş nedir ve konuyu daha iyi kavramanız için yayın yaptığı iş ile ilgili örnekler çözeceğiz. Kuvvetin konumla değiştiği genel bir fiziksel sistem Şekil 1 de gösterilmiş­tir. Pürüzsüz, yatay bir yüzey üzerindeki bir cisim, sarmal bir yaya bağlıdır. Yay, denge konumundan gerilir veya sıkıştırılırsa, cisim üzerine

F_s = – kx  (Eşitlik 1)

ile verilen bir kuvvet uygular. Burada x, cismin gerilmemiş (x = 0) konumuna göre yerdeğiştirmesi, k yayın kuvvet sabiti olarak adlandırılan pozitif bir sabit­tir. Diğer bir deyişle, bir yayı germek veya sıkıştırmak için gerekli kuvvet, geril­me veya sıkıştırmanın x – büyüklüğü ile orantılıdır. Yaylar için Hooke kanunu olarak bilinen bu kuvvet yasası, sadece küçük yerdeğiştirmeler için geçerlidir. Sert yaylar daha büyük, yumuşak yaylar daha küçük k değerlerine sahiptir.

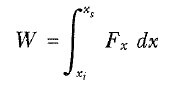
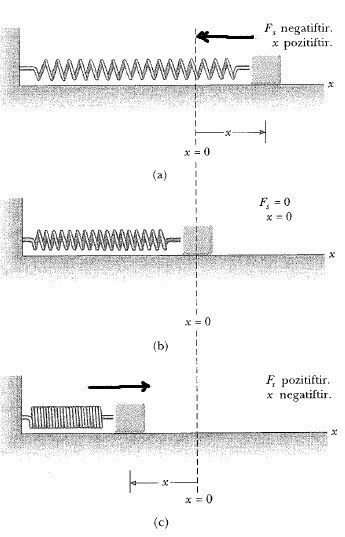
Eşitlik 1 deki eksi işareti, yayın etkidiği kuvvetin daima yerdeğiştirme ile zıt yönlü olduğunu ifade eder. Şekil 1 a’daki gibi x> 0 olduğunda, yay kuv­veti sola, negatif yönüne yönelmiştir. Şekil 1c’deki gibi x < 0 olduğun­da, yay kuvveti sağa yani pozitif x – doğrultusunda yönelir. Şekil 1b deki gi­bi x = 0 olduğunda yay gerilmemiştir ve F_s = 0 dır. Yay kuvveti daima denge ko­numuna doğru etkidiği için, geri çağırıcı kuvvet olarak adlandırılır. Kütle, den­ge konumundan -x_maks  kadar yerdeğiştirilerek serbest bırakıldığında, – x_maks den sıfıra ve oradan  + x_maks ye hareket edecektir. Yay bu kez de, blok x_maks noktasına gelinceye kadar gerdirilir ve sonra bırakılırsa, blok, +x_maks dan, sıfırdan geçerek – x_ınaks ’a hareket eder. Daha sonra yön değiştirerek +x_maks‘a yönelir ve ileri geri titreşimini sürdürür.

Bloğun, denge konumundan sola doğru bir x_maks kadar itildiğini ve son­ra serbest bırakıldığını varsayınız. Blok x_i = – x_maks ’den x_s = 0 ’a hareket eder­ken yay kuvvetinin yaptığı işi hesaplayalım. 2 Eşitliğini uygulayarak

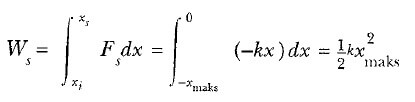
elde ederiz. Burada ∫xⁿdx=xⁿ⁺¹ /(n + 1) belirsiz integralini n  = 1 için kullan­dık. Yay kuvveti yerdeğiştirme ile aynı yönlü olduğu için (her ikisi de sağa doğ­ru) yapılan iş pozitiftir. Bununla birlikte cisim, x_i = 0 ’dan x_s = x_maks ‘a giderken yay kuvvetinin yaptığı işi gözönüne aldığımızda, Ws = 1/2kx_maks² buluruz. Çünkü hareketin bu kısmında, yerdeğiştirme sağa doğru, yay kuvveti sola doğrudur. Dolayısıyla cisim x_i = x_maks ’den x_s = x_maks ‘a giderken yay kuvvetinin yaptığı net iş sıfırdır.

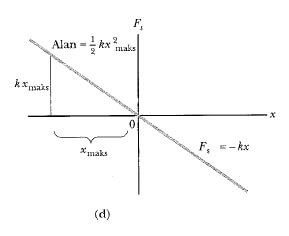
Şekil 1d, x ‘e göre F_s nin grafiğidir. 3 Eşitliğinde hesaplanan iş, göl­geli üçgenin alanı olup – x_maks ‘dan 0 ’a yerdeğiştirmeye karşılık gelir. Üçgenin tabanı , x_maks ve yüksekliği kx_maks olduğu için alanı, 3 Eşitliği ile verilen, yayın yaptığı 1/2kx_maks² işidir.

Kütle x = x_i  ‘den x= x_s ‘ye keyfi bir yerdeğiştirme yaparsa, yay kuvvetinin yaptığı iş

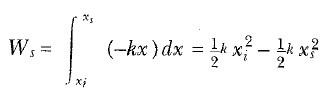
olarak verilir. Örneğin, yay 80 N/m lik kuvvet sabitine sahip olup denge konu­mundan 3 cm sıkıştırılmışsa, bloğun x_i = – 3 cm ‘den, yayın gerilmemiş oldu­ğu x_s = 0 konumuna hareket etmesiyle yayın yaptığı iş, 3,6 x 10^-2 J dür. 4 Eşitliğinden aynı zamanda, başladığı yerde sonlanan (x_i = x_s) herhangi bir ha­reket için yay kuvveti tarafından yapılan işin sıfır olduğunu görüyoruz.

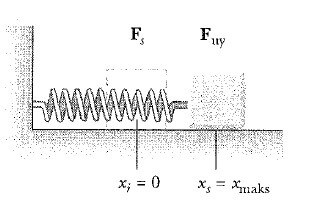
3 ve 4 Eşitlilikleri, yayın blok üzerinde yaptığı işi anlatır. Şimdi Şekil 2 de görüldüğü gibi yayı yavaş yavaş x_i = 0 dan x_s = x_maks ‘a geren bir dış  et­kinin yaptığı işi inceleyelim. Bu iş, uygulanan kuvvetle F_uy, F_s yay kuvvetinin eşit ve zıt yönlü olduğuna dikkat ederek kolayca hesaplanabilir. Bu durumda her­hangi bir x yerdeğiştirmesi için F = – (-kx) = kx olacaktır. Dolayısıyla bu dış kuvvetin yaptığı iş,

olur. Bu iş, aynı yerdeğiştirme için yaptıran yay kuvvetinin yaptığı işin negati­fine eşittir.

Bu yazımızda sizlere Bir Yayın Yaptığı İş Nedir konusunu anlattık. Diğer yazımızda görüşmek üzere.