Benzinli Motorlar ve Dizel Motorlar

Merhaba arkadaşlar bu yazımızda size benzinli motorlar ve dizel motorlar, benzinli ve dizel motorlar modelleri ve benzinli motorların çalışma prensipleri hakkında bilgi vereceğim. Bir benzinli motorda her bir çevrimde altı işlem meydana gelir; bunların beş tanesi Şekil 1’de gösterilmiştir. Bu tartışmamızda sistemimiz, pistonun üs­tünde kalan silindirin iç kısmıdır ve burada, motorun çalışması sırasında tek­rarlanan çevrim oluşur. Verilen bir çevrimde piston, iki kez yukarıya ve aşağı­ya hareket eder. Bu iki aşağı ve iki de yukarı vuruş içeren bir dört vuruşlu çev­rimi temsil eder. Çevrimdeki bu işlemler, PV diyagramı Şekil 2’de göste­rilen bir Otto çevrimine yaklaştırılabilir:

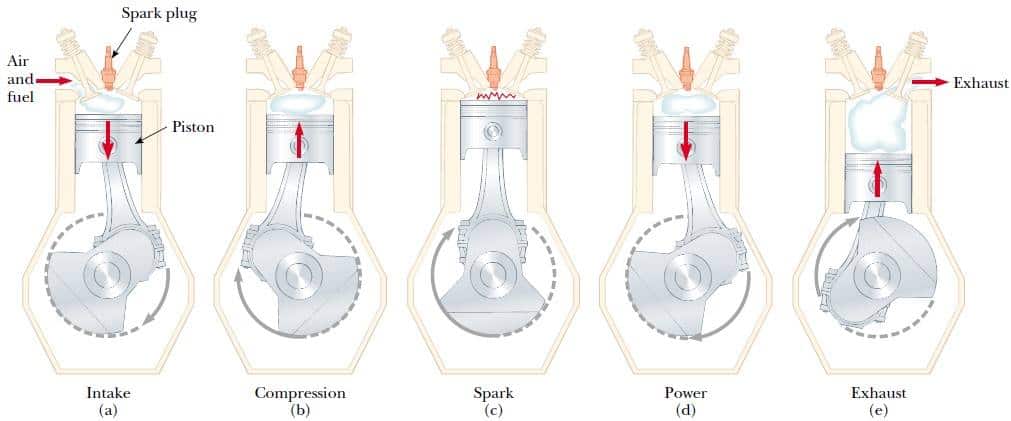
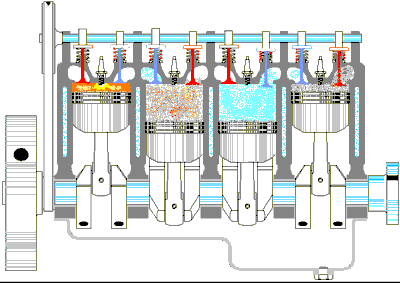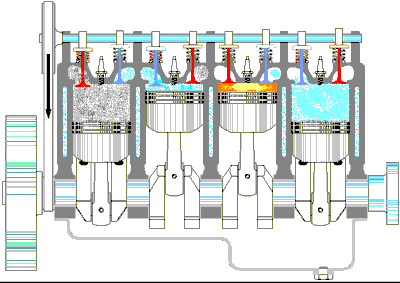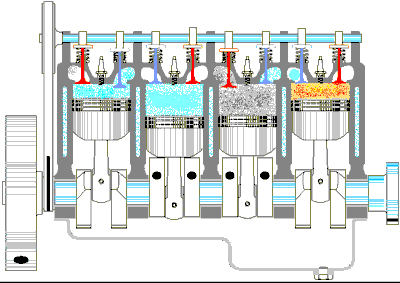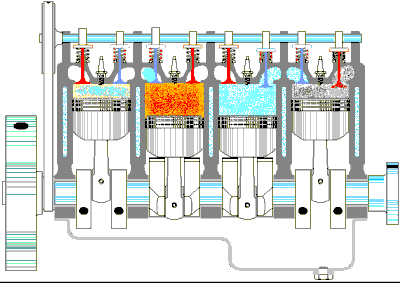
Şekil 1 Standart bir benzin motorunun dört zamanlı çevrimi, (a) Emme zamanında hava ve yakıt karıştırılır, (b) Emme vanası kapanır ve karışım pistonla sıkıştırılır, (c) Karışım bir buji ile ateşlenir ve daha yüksek sıcaklığa çıkar, (d) Güç verme zamanında gaz pistonu iterek genişler. (e) Son olarak artık gaz (egzoz gazı) dışarı atılır ve çevrim tekrarlanır.

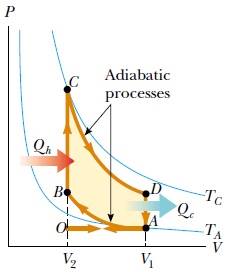
1.O→A emme zamanında (Şekil 1a), piston aşağı hareket eder ve hava ile yakıttan oluşan gaz karışımı atmosfer basıncında silindir içine çekilir, Bu iş­lemde hacim V₂’den V₁’e yükselir. Bu, yakıtta depolanan iç enerjinin siste­me (silindir içine) girmesi nedeni ile çevrimin enerji giriş kısmım oluştu­rur. Bu, enerjinin kütle transferi ile aktarımıdır, yani enerji bir maddede ta­şınmaktadır. Bu, tartıştığımız konveksiyona benzer.

2. A→B sıkıştırma zamanında (Şekil 1b) piston yukarı hareket eder, hava yakıt karışımı V₁, hacminden V₂ hacmine adyabatik olarak sıkıştırılır ve sı­caklık T_A’dan T_B’ye yükselir. Gazın yaptığı iş negatiftir ve değeri Şekil 2’deki AB eğrisinin altındaki alana eşittir.
3. A→B işleminde buji ateşleme yaptığında yanma oluşur (Şekil 1c). Bu, piston en yüksek konumda iken çok kısa bir sürede oluştuğundan, çevrimin bir parçası değildir. Yanma, yakıttaki kimyasal bağlarda depolanan iç ener­jinin sıcaklığa bağlı moleküler hareketin içe enerjisine hızlı bir dönüşümü temsil eder. Bu zaman süresince silindir içindeki basınç ve sıcaklık hızla ar­tar, sıcaklık T_B ’den T_c ’ye yükselir. Fakat zaman aralığı kısa olduğundan hacim hemen hemen sabit kalır. Sonuç olarak gaz hemen hemen hiçbir iş yapmaz. Bu işlemi, Q_h ısı enerjisinin sisteme girdiği bir PV diyagramı ile modelleyebiliriz (Şekil 2). Fakat, gerçekte bu işlem bir transferden çok, (O→A işlemi sebebiyle) silindirde bulunan enerjinin dönüşmesi işlemidir.

4.Güç verme zamanında (Şekil 1d) gaz adyabatik olarak V₂’den V₁’e genleşir. Bu genleşme, sıcakılğırı T_C’den T_D‘ye düşmesine sebep olur. Pistonu aşağı iterek iş yapar ve bu işin değeri CD eğrisi altında kalan alana eşittir.

5.(Şekil 1’de gösterilmeyen) D→A işleminde, bir çıkış (egzoz) vanası, piston, yolunun en alt kısmına ulaştığında açılır ve basınç bu kısa zaman aralığında aniden düşer. Bu zaman aralığında piston hemen hemen dur­gundur ve hacim yaklaşık olarak sabit bir değerdedir. Enerji silindirin için­den dışarıya atılır ve bir sonraki işlem sırasında atılmaya devam eder.

6.Son işlemdeki A→O egzoz zamanında (Şekil 1e) çıkış vanası açık kal­maya devam ederken piston yukarı doğru hareket eder. Kalan gazlar atmos­fer basıncında dışarı atılır ve hacim V₁ ’den V₂ ’ye düşer. Çevrim böylece tekrarlanır.

Hava-yakıt karışımı ideal gaz olarak kabul edilirse, Otto çevriminin verimi,

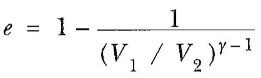
olur. Burada γ yakıt-hava karışımı için molar ısı sığalarının C_p/C_v oranı ve V_l/V₂ ise sıkışma oranıdır. Türettiğimiz eşitlik 22.5, verimin sı­kışma oranı arttıkça artacağını gösterir. Tipik sıkışma oranı 8 ve γ = 1,4 için, ideal bir Otto çevirimine göre çalışan bir makinanın beklenen teorik verimi %56 dır. Bu, gerçek motorlarda ulaşılan verimden (%15’den %20’ye) çok bü­yüktür. Bunun nedeni sürtünme, silindir duvarlarından ısı kaçakları ve tam yanmamış hava-yakıt karışımıdır.

Dizel motorlar Otto çevrimine benzer bir çevrimde çalışır, fakat ateşleyici buji kullanılmaz. Bir dizel motorunun sıkışma oranı benzinli motora göre oldukça yüksektir. Silindirdeki hava çok küçük bir hacme sıkıştırılır ve bunun sonucunda silindirir sıcaklığı oldukça yüksektir. Bu noktada yakıt silindire püskürtülür sıcaklık, yakıt-hava karışımını bujiye ihtiyaç duymadan ateşleyecek kadar yüksektir. Dizel motorları, benzinli motorlara göre yüksek sıkışma oranları ve bundan doğan yüksek sıkışma sıcaklıkları nedeni ile daha verimli­dir.

Benzinli ve Dizel Motorlar Modelleri

Bu ve önceki bölümlerde tartışılan termodinamik ilkeleri­ni, benzinli ve dizel motorların performansını modellemede kullanabiliriz. Her iki motor cinsinde, gaz, ilk olarak motorun silindirinde sıkıştırılır, sonra yakıt-hava karışımı ateşlenir. Gaz üzerinde iş, sıkışma sırasında yapılır, fakat da­ha büyük bir iş, yanma sırasında silindir genleşeceğinden piston üzerinde yapılır. Motorun gücü pistondan krank miline bir kolla aktarılır.

Her iki motorun iki önemli niceliği, piston silindirin dibinden tepesine hareket ettikçe yer değiştirdiği hacim olan yer değiştirme hacmi ve silindirin maksimum ve mini­mum hacimlerinin oranı olan r sıkıştırma oranıdır. Bizim gösterimimizde r =V_A/V_B veya V₁/V₂ ’dir. Bir çok benzinli ve dizel motor, em­me ve atma (egzoz) zamanlarında yapılan net iş ihmal edi­lebilecek kadar küçük olduğundan bir dört-zamanlı işlem­le (emme, sıkıştırma, güç sağlama, atma) çalışırlar. Böylece güç, krank milinin iki devrinden sadece birinde üretilir.

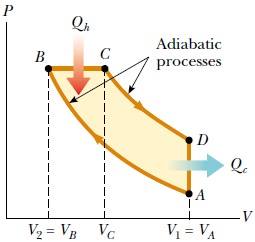
Bir dizel motorunda, sıkıştırma başlangıcında silindir içinde (yakıt olmaksızın) sadece hava bulunur. Şekil 3’teki ideal dizel çevriminde, silindirdeki hava  A ’dan B ’ye bir adyabatik sıkışmaya uğrar. B noktasında yakıt silindir o şekilde püskürtülür ki, yakıt karışımı sabit basınçta bir ara V_C(B→C) hacmine genleşir. Karışımın yüksek sıcaklığı yanmaya sebep olur ve güç zamanı V_D = V_A (C→D) ’ye doğ­ru bir adyabatik genleşme olur. Çıkış supabı açılır ve silin­dir boşaldıkça bir sabit hacimli enerji çıkışı (D→A)me­ydana gelir. Hesaplamalarımızı basitleştirmek için silindir içindeki karışımın hava dolu bir ideal gaz olduğunu varsa­yalım. C molar özgül ısısı yerine c özgül ısısını kullanacak ve bunun 300K ’de hava için sabit değerde olduğunu varsa­yacağız. Özgül ısı ve evrensel gaz sabitini mol yerine birim kütleler cinsinden ifade edeceğiz. Böylece, C_V = 0,718kJ/kg.K, C_P = l,005kJ/kg.K, γ=C_P/C_V=1,40 ve R= C_P – C_V = 0,287kJ/kg.K = 0,287kPa.m³/kg.K değerlerini elde ederiz.

3 L’lik Benzinli Motor

3 L’lik bir yer değiştirme hacmine sahip 4000 rpm (de­vir/dk) da çalışan ve r = 9,50 ’lik bir sıkıştırma oranına sa­hip 6 silindirli benzinli bir motorun ürettiği gücü hesapla­yalım. Hava-yakıt karışımı silindire atmosfer basıncında gi­rer ve ortamın sıcaklığı 27°C ’dir. Patlama (yanma) sırasın­da karışımın sıcaklığı 1350°C ’a ulaşmaktadır.

Önce her bir silindirin yaptığı işi hesaplayalım. Başlan­gıç basıncını P_A = l00kPa ve sıcaklığı T_A = 300K alarak baş­langıç hacmini ve hava-yakıt karışımının kütlesini hesapla­yabiliriz. İlk ve son hacimlerinin oranının sıkıştırma oranı olduğunu biliyoruz:

V_A/V_B = r = 9,50

Ayrıca, hacim farkının yer değiştirme hacmi olduğunu da biliyoruz. 3 L ’lik bir motor hacmi, altı silindirin hepsinin kullandığı hacimdir. O halde silindir için

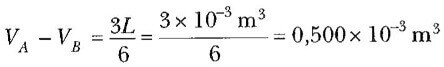
olur. Bu iki eşitliği birlikte çözerek ilk ve son hacimleri bu­luruz:

V_A= 0,559 x 10^-3 m³       V_B = 0,588 x 10^-4 m³

ideal gaz kanununu (mol yerine kütle cinsinden evrensel gaz sabitini kullandığınızdan P_v= mRT formunda) kulla­nırsak, hava-yakıt karışımının kütlesini bulabiliriz:

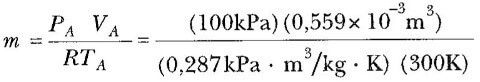
A→B işlemi  bir adyabatik sıkıştır­madır ve bu PV^γ = sabit anlamına gelir; buradan

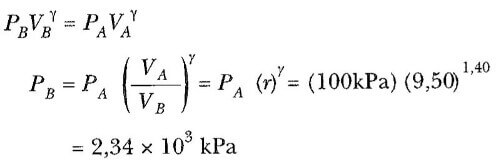
bulunur. İdeal gaz kanunu kullanılırsa sıkıştırma sonunda sıcaklık,

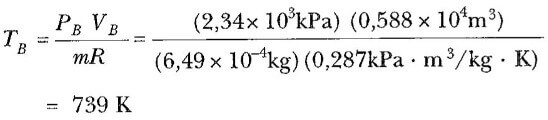
olur.

B→C işleminde yanma, kimyasal bağlardaki iç enerji­yi, sabit hacimde yani V_c = V_B de moleküler hareketin iç enerjisine dönüştürür. Patlama, sıcaklığın T_c = 1350°C = 1623K ’e yükselmesine sebep olur. Bu değeri ve ideal gaz kanununu kullanarak P_c ’yi hesaplayabiliriz:

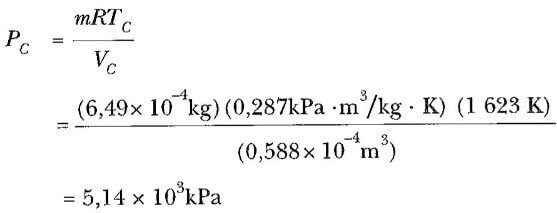
C→D işlemi bir adyabatik genleşmedir; genleşme sonrası basınç,

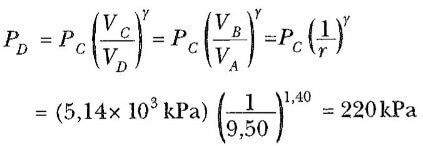
olur. Yine ideal gaz kanununu kullanarak son sıcaklığı bu­labiliriz:

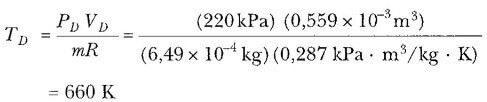
Şimdi, her bir çevrimin ilk ve son sıcaklıklarını biliyo­ruz. Artık, herbir silindir tarafından her iki çevrimde yapı­lan net iş ve net enerji transferini hesaplayabiliriz. Eşitlik 21.8’den

Q_h = Q_giriş = mc_v(T_C – T_B)

= (6,49 x 10^-4kg) (0,718 kJ/kg.K) (1623K- 739K) = 0,412 kj

Q_C = Q_çıkış = mc_v(T_D – T_A)

= (6,49 x 10″⁴ kg) (0,718 kJ/kg.K) (660K – 300K) = 0,168 kj

W_net= Q_giriş – Q_çıkış = 0,244 kj

bulunur. Eşitlik den verim e= W_net/Q_giriş = %59 olarak bulunur (Eşitlik 22.5 ’den verimi doğrudan sıkışma oranın­dan da hesaplayabilirdik).

Gücün, krank milinin iki dönüşümünde dağıtıldığını hatırlarsak, 4000dev/dak hızla çalışan altı silindirli moto­run net gücü

Pnet = 6(1/2dev) (4000 dev/dak) (1 dak/60s) (0,244 kj)

= 49 kW = 66 hp (B.G)

olur.

2L’lik Dizel Motoru

2,00L yerdeğiştirme hacmi olan ve 3000dev/dk ’da çalışan bir dört silindirli dizel motorun ürettiği gücü hesaplayalım. Sıkıştırma oranı r  = V_A/V_B = 22 ve Şekil 22.13 ’teki B→C sabit-hacimli işlem sırasında hacim değişimi oram olan kes­me oranı r_c= V_C/V_B = 2 ’dır. Hava her silindire atmosfer ba­sıncı ve 27°C ’lik ortam sıcaklığında sıkıştırma çevriminin başında girmektedir.

Dizel motoru modelimiz, benzinli motorunkine ben­zer; şu farkla: dizelde yakıt B noktasında püskürtülür ve A→B sıkıştırma çevriminin sonunda sıcaklık, tutuşma dere­cesine ulaştığında karışım kendi kendine ateşlenir. Burada enerji girişinin B→C sabit-basınç işleminde oluştuğunu ve genleşme işleminin C ’den D ’ye ısı yoluyla başka bir enerji transferi olmaksızın devam ettiğini varsayıyoruz.

İlk hacmi V_A = (2 x 10^-3m³)/4 = 0,500 x 10^-3m³ olan her bir silindirin yaptığı işi hesaplayalım. Sıkıştırma oram oldukça yüksek olduğundan, maksimum silindir hacmi yak­laşık yer değiştirme hacmi kadar olsun. İlk basınç P_v = 1000 kPa ve ilk sıcaklık T_A = 300 K olursa, ideal gaz kanununu kullanarak silindirdeki havanın kütlesini hesaplayabiliriz:

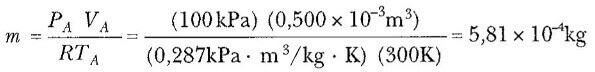
A→B işlemi bir adyabatik sıkıştırmadır, böylece PV^γ = sa­bittir. Buradan,

P_BV_B^γ = P_AV_A^γ

P_B = P_A (V_A/V_B)^γ = (100kPa) (22)^1,10 =7,57×10 ³ kPa

olur. İdeal gaz kanununu kullanarak sıkıştırmadan sonra havanın sıcaklığını

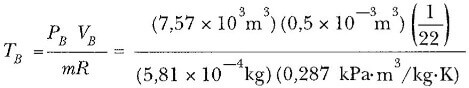
olarak buluruz.

B→C işlemi bir sabit basınçlı genleşmedir; o halde P_c = P_B olur. 2 ’lik kesme oranından, hacmin bu işlemde iki katma çıktığını biliriz. İdeal gaz kanununa göre bir izobarik işlemdeki hacmin iki katma çıkması, sıcaklığın da iki ka­tma çıkması anlamına gelir. Dolayısı ile

T_C=2T_B= 2,06 x 10³K

olur. C→D işlemi bir adyabatik genleşmedir. Buna göre

elde edilir. İdeal gaz kanunundan D ’deki sıcaklığı bulabi­liriz:

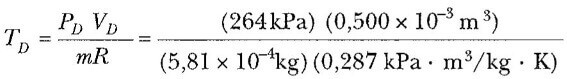
Şimdi herbir işlemin ilk ve son sıcaklıklarım bildiğimizden her iki çevrimde herbir silindir tarafından yapılan net işi ve ısı yolu ile yapılan net enerji transferini hesaplayabiliriz.

Q_h = Q_giriş = mc_p(T_C – T_B) = 0,601 kj

Q_C = Q_çıkış = mc_v(T_D – T_A) = 0,205 kj

W_net= Q_giriş – Q_çıkış = 0,396 kj

Verim e= W_net/Q_giriş = %66 ’dır.

3000dev/dk ’da çalışan dört silindirli bir motorun net gücü,

P_net = 4(1/2dev) (3000 dev/dak) (1 dak/60s) (0,396 kj)

= 39,6 kW = 53 (B.G) hp

dir. Tabii ki modern motor tasarımları, idealleştirilmiş çev­rimleri kullanan bizim termodinamik uygulamanın ötesin­dedir.

Benzinli motorlar ve dizel motorlar ile ilgili yararlı bir video.