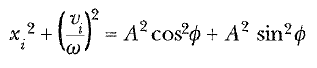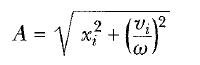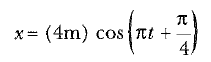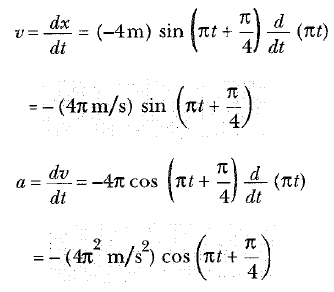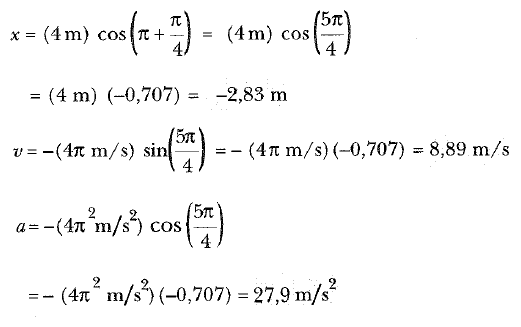Basit Harmonik Hareket Konu Anlatımı

Merhaba arkadaşlar bu yazımızda sizlere basit harmonik hareket konu anlatımı ve basit harmonik hareket ile ilgili sorular çözeceğiz. Bir yayın ucuna tutturulmuş m kütleli bir bloğun yatay, sürtünmesiz yüzey üzerinde serbestçe hareket edebildiği fiziksel bir sistemi inceleyelim (Şekil 1). Yay gerilmemiş ve sıkıştırılmamış durumda iken blok, sistemin denge konumu denilen x = 0 konumundadır. Böyle bir sistem denge konumundan uzaklaştırıldığında, ileri-geri salınım yaptığını deneyimlerimizden biliriz.

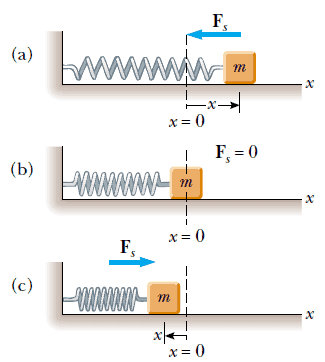
Şekil 1: Bir yaya tutturulmuş, sürtünmesiz yüzey üzerinde hareket eden blok, (a) Blok dengenin sağına (x > 0) kaydırıldığında, yay tara­fından uygulanan kuvvet sola doğru etkir, (b) Blok denge konumunda iken (x= 0), yayın uyguladığı kuvvet sıfırdır, (c) Blok dengenin soluna (x < 0) kaydırıldığında, yay tarafından uygulanan kuvvet sağa doğru etkir.

İlk blok, denge konumundan küçük bir x uzaklığı kadar uzaklaştırıldığın­da yay, blok üzerine yer değiştirme ile orantılı ve Hooke yasası ile verilen

F_s = -kx (Eşitlik 1)

şeklinde bir kuvvet uyguladığını hatırlayarak, Şekil 1 deki hareketi nitel ola­rak anlayabiliriz. Daima denge konumuna doğru yöneldiği ve bu yüzden yer değiştirmeye zıt olduğu için buna geri-çağırıcı kuvvet deriz. Yani blok, Şekil 1 de x = 0 in sağına gittiğinde, yer değiştirme pozitiftir ve geri çağırıcı kuvvet sola doğru yönelir. Blok x = 0 ın soluna gittiğinde, yer değiştirme negatiftir ve geri-çağırıcı kuvvet sağa doğru yönelmiştir.

Eşitlik 1 le birlikte, Newton’un ikinci yasasını bloğun hareketine uygu­larsak,

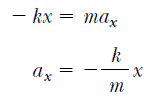
elde ederiz. Yani ivme, bloğun yer değiştirmesi ile orantılıdır ve yönü, yer değiştirmenin yönüne zıttır. Bu şekilde davranan sistemlerin basit harmonik ha­reket yaptıkları söylenir. Cismin ivmesi, cismin bir denge konumundan olan yer değiştirmesi ile orantılı olduğu ve zıt yönde yöneldiği her durumda cisim basit harmonik hareket yapar.

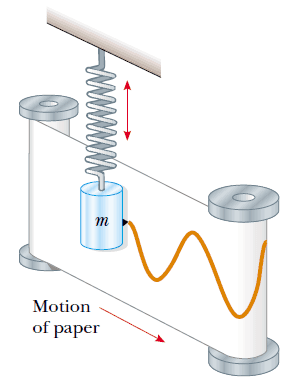
Şekil 2: Basit harmonik hareket gösteren deneysel bir düzenek. Titreşen kütleye tutturulmuş olan bir kalem, hareketli grafik kağıdı üzerine dalgaya benzer bir desen çizer.

Basit harmonik hareket sergileyen deneysel bir düzenek Şekil 2 de gösterilmektedir. Yaya bağlı ve düşey olarak titreşen kütleye bir kalem tutturulmuştur. Kütle salınım yaparken, bir kağıt hareket doğrultusuna dik yönde kay­dırılır ve kalem dalga şeklinde bir desen çizer.

Genelde, x ekseni boyunca hareket eden bir parçacığın, denge konumun­dan ölçülen x yer değiştirmesi

x = Acos(ωt + Φ) (Eşitlik 3)

bağıntısına göre zamanla değişirse, basit harmonik hareket yapıyor denir; burada A, ω ve Φ sabittir. Bu sabitlerin fiziksel anlamları, Şekil 3a da x ’i t nin fonksiyonu olarak çizilerek gösterilmiştir. Bu tam şekil 2 de gösterilen deneysel aletle gözlenen desendir. Hareketin genliği olan A, parçacığın pozitif x veya negatif x yönündeki en büyük yer değiştirmesidir. ω sabiti hareketin açı­sal frekans adını alır ve saniyede radyan birimindedir. (ω nin geometrik öne­mini diğer yazılarımız da tartışacağız) Sabit açı Φ ye faz sabiti (veya faz açısı) denir ve parçacığın başlangıç yerdeğiştirmesi ve hızından tayin edilir. Eğer parçacık t = 0 da x = A maksimum konumunda ise, bu takdirde Φ=0 dır ve x in t ye gö­re eğrisi Şekil 3b de gösterildiği gibidir. Parçacık t = 0 da başka bir konum­da ise, Φ ve A sabitleri bize, t = 0 anında yer değiştirmenin ne olduğunu söyler. (ωt + Φ) büyüklüğüne hareketin fazı denir ve iki parçacıklı sistemlerin yaptığı hareketlerin karşılaştırılmasında faydalıdır.

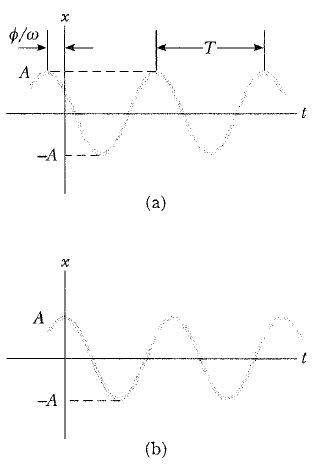
x fonksiyonunun periyodik olduğuna ve ωt nin, 2π radyan artmasıyla ken­dini tekrarladığına dikkat edilmelidir. T periyodu, parçacığın hareketinin bir tam devrini tamamlaması için gereken süredir. T nin bu tanımı bize x in t anın­daki değerinin, x in t + T anındaki değerine eşit olduğunu söyler. T kadarlık süre içinde (ωt + Φ) fazın 2π radyan arttığı önceki gözlemimizi dikkate alarak, T = 2π/ω olduğunu gösterebiliriz:

ωt + Φ + 2π = ω.(t + T) + Φ

buradan, ωT = 2π veya

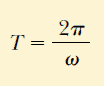
Periyodun tersine, hareketin f frekansı denir. Frekans, parçacığın birim zamanda yaptığa titreşimlerin sayısını gösterir:

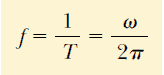
f nin birimleri devir/s, veya hertz (Hz) dir. Ayrıca Eş 13.5’ten:

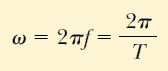
açısal frekansını elde ederiz.

Basit, harmonik hareket yapan bir parçacığın hızını, 1. eşitliğinin zamana göre türevini alarak bulabiriz:

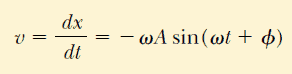
parçacığın ivmesi

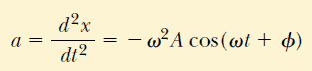
dir. x = Acos(ωt + Φ) olduğu için, 8 Eşitliği şöyle olur:

a = -ω²x (Eşitlik 9)

Sinüs fonksiyonu = ±1 arasında değiştiği için, Eşitlik 7, v’nin uç değerlerini ±ωA olarak verir. Kosinüs-fonksiyonu da ±1 arasında değiştiği için Eş. 6 ivmenin uç değerlerinin ±ω²A olduğunu söyler. Bu nedenle, basit harmonik hareket yapan bir parçacık için hız ve ivmenin maksimum değerleri:

v_maks = ωA (Eşitlik 10)

a_maks = ω²A (Eşitlik 11)

ile verilirler.

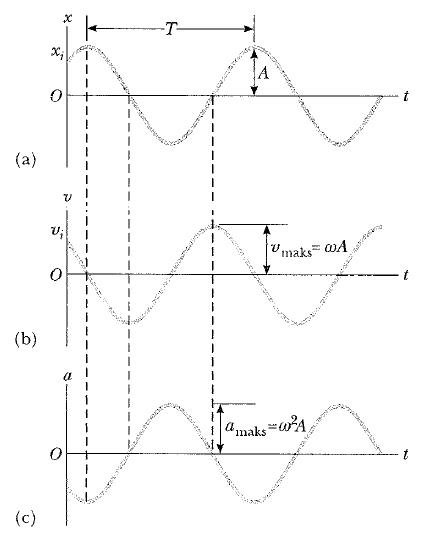
Şekil 4:Basit harmonik hareketin grafiksel gösterimi: (a) Zamana göre yerdeğiştirme, (b) Zamana göre hız ve (c) Zamana göre ivme. Herhangi belirli bir zamanda hızın, yer değiştirme ile 90°, ivmenin yer değiştirme ile 180° faz farkı olduğuna dikkat ediniz.

Şekil 4a, keyfi bir faz sabiti için yerdeğiştirme-zaman eğrisini göstermektedir. Hız ve ivme eğrileri Şekil 4b ve c de gösterilmiştir. Bu eğriler; hız fazının, yerdeğiştirme fazından π/2 rad, ya da 90° farklı olduğunu gösterir. Yani x, en büyük veya en küçük değerde iken hız sıfırdır. Benzer şekilde, x sıfır iken hız en büyüktür. Dahası ivme fazı, yerdeğiştirme fazından π radyan veya 180° kadar farklıdır. Yani, x en büyük değerde iken, a zıt yönde en büyük değerdedir.

Faz sabiti, iki veya daha fazla sayıda titreşen cismin hareketlerini karşılaştırırken önemlidir. Birisi diğerinden daha sonra serbest bırakılmış olan iki sarkaç topunun yan yana salınarak basit harmonik hareket yaptıklarını düşünelim. Sarkaç topları farklı faz sabitine sahiptirler. Parçacığın başlangıç hızı ve konumu ile hareketin açısal frekansını bildiğimiz takdirde, harmonik hareket yapan parçacıklardan her birinin faz sabiti ve genliğinin nasıl belirlenebileceğini gösterelim.

Varsayalım ki, t = 0 da tek bir sallanın ilk konumu x = x_i ve ilk hızı v = v_i dir. Bu koşullar altında, Eşitlik 3 ve 7 den

x_i = AcosΦ (Eşitlik 12)

v_i = -ω AsinΦ (Eşitlik 13)

yazılabilir. Eşitlik 13 Eşitlik 12 ye bölünürse A yok olur ve v_i/x_i = -ω tanф, veya

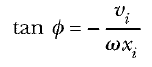
elde edilir. Ayrıca, Eşitlik 12 ve 13 ün karelerini alıp, hız denklemini ω² ile bölüp daha sonra terimleri toplarsak

elde ederiz, sin²ф + cos²ф = 1 özdeşliğini kullanarak A yı çözebiliriz:

Basit Harmonik Hareket Yapan Bir Parçacığın Önemli Özellikleri

1. Denge konumundan olan yer değiştirme, hız ve ivme zamanla sinüsel olarak değişir, fakat Şekil 4 te gösterildiği gibi, aynı fazda değildirler.
2. Parçacığın ivmesi, yer değiştirme ile orantılı fakat zıt yöndedir. Tüm diğer çeşit titreşimlerin aksine bu, basit harmonik hareket için gerek ve yeter şartıdır.
3. Hareketin frekansı ve periyodu genlikten bağımsızdır.

Basit Harmonik Hareket İle İlgili Sorular

Bir cisim, x ekseni boyunca basit harmonik hareket yapıyor. Başlangıç noktasından itibaren yer değiştirmesi zamanla

denklemine göre değişiyor, burada t s cinsinden zaman ve parantezin içindeki açılar radyan cinsindendir. (a) Hareketin genliğini, frekansını ve periyodunu bulunuz.

Bu denklemi basit harmonik hareket için genel bağıntı olan, x = Acos(ωt + Φ) ile karşılaştırarak A = 4m ve ω = π rad /s olduğunu görürüz. O halde f = ω/2π = π/2π = 0,50 Hz ve T = 1/f = 2s buluruz.

(b) Cismin herhangi bir t anındaki hızını ve ivmesini hesaplayınız.

(c) (b) kısmının sonuçlarını kullanarak cismin t = 1s deki konumunu, hızını ve ivmesini bulunuz.

Çözüm: Trigonometrik fonksiyonlarda açıların radyan cinsinden verildiğine dikkat ederek, t = 1s için;