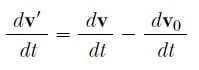Bağıl Hız Konu Anlatımı

Merhaba arkadaşlar bu yazımızda sizlere bağıl hız konu anlatımı ve bağıl hız formüllerini açıklayacağız. Bağıl hız nedir; birbiriyle bağlantılı olan farklı referans sistemlerindeki farklı gözlemciler tarafından gözlemlerin nasıl yapıldığını tanımlıyoruz. Farklı referans sistemlerindeki gözlemcilerin verilen bir parçacık için farklı yerdeğiştirmeler, hızlar ve ivmeler ölçebildiğini buluruz. Yani birbirlerine göre hareketli iki gözlemci, ölçümlerinin sonuçlarında genel olarak hemfikir olmazlar.

Örneğin, iki otomobilin 50 mi/saat ve 60 mi/saat lik hızlarla aynı yönde hareket ettiklerini varsayalım. Yavaş olan otomobildeki bir yolcuya göre, süratli otomobilin hızı 10 mi/saat ’tir. Kuşkusuz, duran bir gözlemci daha hızlı olan otomobilin süratini 10 mi/saat değil 60 mi/saat olarak Ölçecektir. Hangi gözlemci haklıdır? Onların her ikisi de haklıdır! Bu basit örnek bir cismin hızının onun içerisinde ölçüldüğü referans sistemine bağlı olduğunu gösterir.

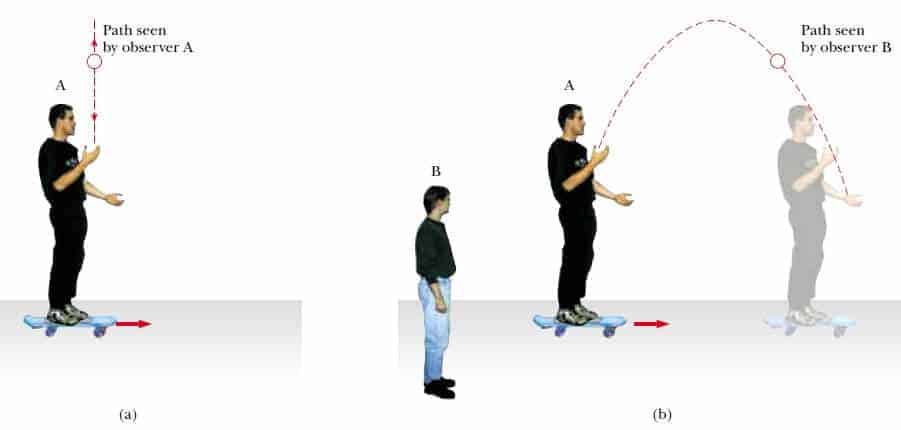
Kaykay süren bir kişinin (A gözlemcisi) Şekil 1a da gösterildiği gibi, bir topu kendisinin referans sisteminde önce bir doğru boyunca yukarıya ve sonra aynı düşey çizgi boyunca aşağıya doğru hareket etmekteymiş gibi görünecek şekilde fırlattığını varsayalım. Duran bir gözlemci (B) Şekil 1b ’de gösterildiği gibi, topun yolunu bir parabol olarak görecektir. B gözlemcisine göre, topun (yukarıya doğru olan ilk hızdan ve aşağıya doğru olan çekim ivmesinden sonuçlanan) düşey bir hız bileşeni ve yatay bir hız bileşeni vardır.

Bu kavramın basit bir örneği, sabit hızla uçan bir uçaktan bir paket atılması örneğidir. Uçaktaki gözlemci paketin hareketini yere doğru düz bir çizgi olarak görür. Ancak, yerde bulunan bir kaşif, paketin havada çizdiği yolu bir parabol olarak görecektir. Bir kere paketi attıktan sonra, eğer uçak aynı hızla yatay olarak hareket etmeye devam eder­se, paket (sürtünmenin ihmal edildiğini kabul edersek) uçağın tam altında ye­re çarpacaktır!

Bağıl Hız Formülleri

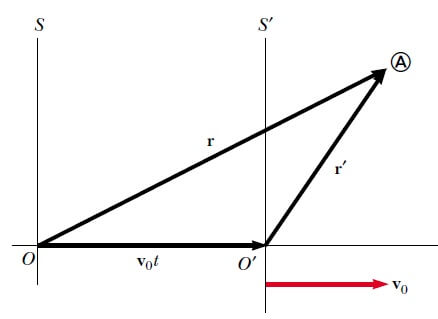
Daha genel bir durumda, Şekil 2 ’de A noktasına yerleşmiş bir parça­cığı göz önüne alalım. Bu parçacığın hareketinin biri, yere göre sabit S refe­rans sisteminde ve diğeri sabit bir v₀ hızıyla S’ye göre aşağa doğru (dolayısıy­la yeryüzüne göre) hareket eden S’ referans sisteminde bulunan iki gözlemci tarafından tanımlandığını düşünelim. (S’ ‘deki bir gözlemciye göre, S bir v₀ hızıyla sola doğru hareket eder.) Gözlemcinin referans sistemindeki yeri bu tartışmada anlamsızdır, fakat bu tartışmanın amaçları için herbir gözlemci kendi orjinine yerleştirilebilir.

Parçacığın, S sistemine göre konumunu r konum vektörüyle ve belli bir t zaman sonra, S sistemine göre konumunu r’ vektörüyle belirleyelim, r ve r’ vektörleri birbirine r = r’ + v₀t veya r’ = r – v₀t (Eşitlik 1) eşitliğiyle bağlıdır. Yani, bir t zaman sonra S’ sistemi sağa doğru v₀t miktarı kadar yer değiştirir.

1 Eşitliğinin zamana göre türevini alır ve v₀ ’ın sabit olduğuna dikkat edersek,

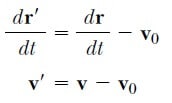
elde ederiz. Burada v’, parçacığın S’ sisteminde gözlenen ve v₀ S sisteminde gözlenen hızdır. 1 ve 2 Eşitlikleri Galile dönüşüm denklemleri olarak bilinir. Bu denklemler, Yeryüzü’ne göre sabit olan bir sistemde ölçüldüğü gibi, bir parçacığın koordinatlarını ve hızını yeryüzüne göre düzgün bir şekilde hareket eden bir sistemde ölçülen koordinatlar ve hızla ilişkilendirir.

Her ne kadar farklı iki referans sistemindeki gözlemciler, parçacıklar için farklı hızlar ölçerlerse de, v₀ sabit olduğu zaman aynı ivmeyi ölçeceklerdir. Bunu

şeklinde 2 Eşitliğinin zamana göre türevini alarak sağlamasını yapabiliriz. v₀ sabit olduğundan, dv₀/dt = 0 ’dır. O nedenle a’ = dv’/dt ve a = dv/dt oldu­ğundan a’ = a sonucuna varırız. Yani, parçacığın, yeryüzünün referans siste­mindeki bir gözlemci tarafından ölçülen ivmesi, yeryüzünün referans sistemi­ne göre sabit hızla hareket eden herhangi bir gözlemci tarafından ölçülen iv­meyle aynı değerde olacaktır.

Bağıl Hız İle İlgili Örnek

Kuzeye yönelen bir tekne, geniş bir nehri suya göre 10 km/saat ’lik bir hızla karşıdan karşıya geçmektedir. Nehirdeki su doğuya doğru yere göre 5 km/saat ‘lik düzgün bir hıza sahiptir. Teknenin kıyılardan birinde duran bir gözlemciye göre hızını bulunuz.

Çözüm: v_tn ‘teknenin nehre göre ve v_nY ’nin nehirin yere göre hızı oluğunu biliyoruz. Bulmak istediğimiz tek­nenin yere göre olan v_tY hızıdır. Bu üç nicelik arasındaki bağıntı

v_tY = v_tn + v_nY

dir. Denklemdeki terimler vektörel nicelikler olarak ele alınmalıdır; vektörler Şekil 2 de gösterilmektedrir. V_tY niceliği kuzeye, v_nY doğuya doğrudur ve iki vektörün vektörel toplamı olan v_tY Şekil ’de tanımlandığı gibi bir Θ açısıyla yönelir. Böylece teknenin yere göre olan hızının büyüklüğünü Pisagor teoremini kullanarak bulabiliriz:

dır. Tekne 11,2 km/saat hızla yere göre 26,6⁰ kuzey doğu yönünde yol alacaktır.