
Oersted’in sapan pusula iğnesi hakkında 1819’daki keşfi, akım taşıyan bir telin bir manyetik alan oluşturduğunu apaçık gösterir. Bu deneyde, bir çok pusula iğnesi şekilde ki gibi uzun düşey bir tele yakınca yatay bir düzleme konur. Telde hiçbir akım olmadığı zaman, ilmekteki tüm pusulalar aynı yönde (yerin alanı yönünde) yönelirler. Bu doğal olarak beklenen bir olgudur. Ancak, telden kuvvetli kararlı bir akım geçerse, şekil b’de görüldüğü gibi, tüm pusula iğneleri çembere teğet olacak yönde saparlar. Bu gözlemler, akımın oluşturduğu В’nin yönünün sağ-el kuralı ile uyumlu olduğunu gösterir. Akımın yönü tersine çevrilirse, şekil b’deki pusula iğneleri de tersine dönerler.
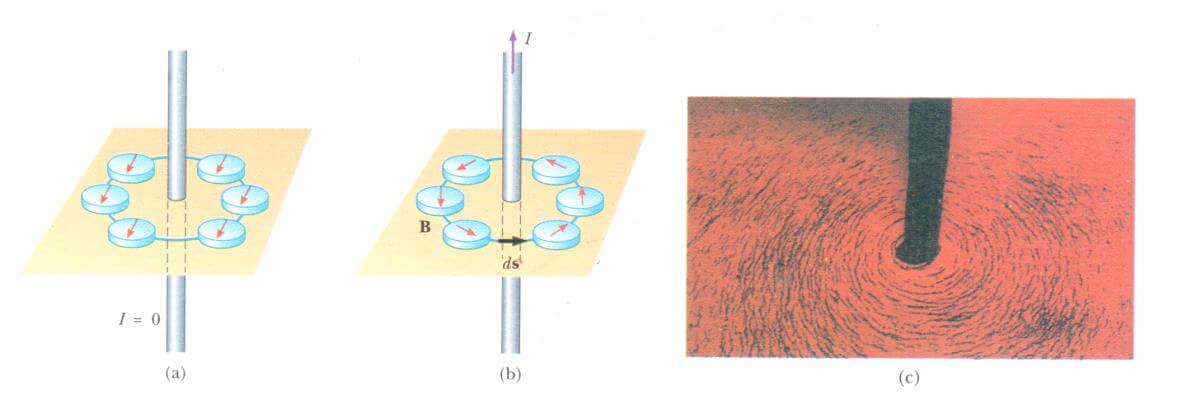
(Dünyanın kuzey kutbuna doğru), (b) telden kuvvetli bir akım geçtiğinde, pusula iğneleri çembere teğet olan yönde saparlar. Bu yön, akımın oluşturduğu manyetik alanın yönüdür, (c) Akım taşıyan bir iletkeni saran çembersel manyetik alan çizgilerinin demir tozları ile görüntülenmesi. (Нету Leap ve Jim Lehman’m izniyle)
Pusula iğneleri В nin yönünde yöneldiklerinden, önceki kesimde tartıştığımız gibi, В nin alan çizgilerinin teli eksen kabul eden çemberler oluşturdukları sonucuna ulaşırız. Simetriden ötürü, В nin büyüklüğü, tele dik olan bir düzlem içinde kalan ve merkezi tel üzerinde olan çembersel bir yol üzerindeki her yerde aynıdır.
Şimdi, В • ds çarpımını hesaplayıp bu çarpımların, pusula iğnelerinin tanımladığı çembersel yolun üzerindeki ds uzunluk elemanları için çembersel kapalı yol üzerinden toplamını alalım. Bu yol boyunca dsveB vektörleri birbirlerine paraleldir (şekil b), bu yüzden В ■ ds = В ds dir. Bu nedenle, kapalı yol boyunca В ds çarpımlarının toplamı, ki bu toplam В • ds nin çizgi integraline eşdeğer olup aşağıdaki bağıntı ile verilir.
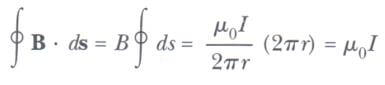
Burada ∫ ds = 2πr çemberin çevresidir. Bu sonuç, bir teli çevreleyen özel bir çembersel yol durumu için elde edilmiş olmasına rağmen, zamanla değişmeyen (kararlı) bir akımı çevreleyen keyfi biçimli bir kapalı yol için de geçerlidir. Ampere Yasası olarak bilinen genel durum şöyle söylenebilir:
”Herhangi bir kapalı yol çevresinde В • ds’nin çizgi integrali μ0.I ’eşittir. Burada I kapalı yolun çevrelediği herhangi bir yüzeyden geçen toplam sürekli akımdır”
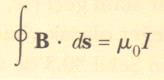
Ampere yasası tüm sabit akım şekillenimlerinin oluşturduğu manyetik alanları betimler, ancak matematik seviyemiz yalnız oldukça yüksek simetriye sahip alan akım şekillerinin manyetik alanlarını hesaplamamıza uygundur. Kullanılışı, oldukça simetrik olan yük dağılımlarının oluşturduğu elektrik alanlarının hesaplanışındaki Gauss Yasasına benzer.

