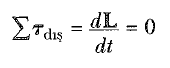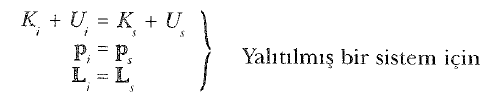Merhaba arkadaşlar bu yazımızda sizlere açısal momentumun korunumu hakkında bilgiler vereceğiz. Parçacıklardan oluşan bir sistemin toplam doğrusal momentumunun, sisteme etki eden bileşke dış kuvvetin sıfır olması halinde, sabit kalacağını biliyoruz. Benzeri bir korunum yasası da dönme hareketi için vardır: Eğer bir sisteme etki eden bileşke dış tork sıfırsa, sistemin toplam açısal momentumunun büyüklüğü ve doğrultusu sabittir.
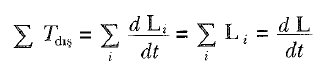
Bunun böyle olduğu 1 Eşitliğinde doğrudan görülebilir: Yani, eğer
ise L = sabit
olur. Bir parçacıklar sistemi için, bu korunum yasasını,∑Ln = sabit olarak yazarız. Burada n alt indisi sistemdeki n ’inci parçacığı gösterir.
Bir cismin kütlesi kendi içinde yeni bir dağılıma uğrarsa, o zaman cismin eylemsizlik momenti değişir ve bunun sonucu olarak da cismin açısal hızı değişmelidir, çünkü L = IW dır. Bu durumda, açısal momentumun korunumunu
Li = Ls = sabit (eşitlik 2)
olarak ifade ederiz.
Sistem sabit bir eksen (örneğin z ekseni) etrafında dönen bir cisim ise, Lz = lW yazabiliriz. Burada Lz, L nin dönme ekseni doğrultusundaki bileşeni ve I, bu eksene göre eylemsizlik momentidir. Bu durumda açısal momentumun korunumu yasası,
IiWi = IsWs = sabit
olarak ifade edilir. Bu ifade, sabit bir eksen etrafındaki dönme ve hareketli bir sistemin kütle merkezinden geçen ve hareket boyunca doğrultusu değişmeyen bir eksen etrafındaki dönmenin her ikisi için de geçerlidir. Bunun için gerekli olan tek şey, net dış dönme momentinin sıfır olmasıdır.
Kütle merkezine göre açısal momentumla ilgili, burada ispatlamayacağımız, önemli bir teorem vardır. Bu teoremin ifadesi şudur: Kütle merkezinden geçen bir eksene göre, bir cisim üzerine uygulanan bileşke tork, kütle merkezinin, hareketine bakılmaksızın, açısal momentumun zamanla değişimine eşittir.
Bu teorem, kütle merkezi ivmelense bile, т ve L kütle merkezine göre hesaplanması halinde her zaman uygulanabilir. 2 Eşitliğiyle, listemize üçüncü bir korunum yasası eklemiş olduk. Dahası şimdi, yalıtılmış bir sistemin enerjisi, doğrusal momentumu ve açısal momentumunun hep sabit kalacağını söyleyebiliyoruz:
Açısal Momentumun Korunumu Hakkında Örnekler
Açısal momentumun korunumu hakkında birçok örnek vardır. Bir program sonunda dönme hareketi yapan bir buz kayakçısını gözlemişsinizdir. Kayakçının açısal hızı, elleri ve ayaklarını vücuduna yaklaştırdığında büyür. Çünkü bu durumda 1 küçülür. Kayakçı ve buz arasındaki sürtünme ihmal edildiğinde, kayakçıya etki eden dış torkun olmadığını görürüz. Açısal hızın değişmesi, açısal momentumun korunmasını sağlar ve IW çarpımı sabit kalır.
Yine, kayakçının eylemsizlik momentindeki bir azalma, onun açısal hızının artmasına sebep olur. Benzer şekilde, dalgıçlar veya göstericiler değişik hareketler yapmak istediklerinde, daha büyük hızlarda dönmek için ellerini ve ayaklarını vücutlarına yaklaştırırlar. Böylece, yerçekiminden kaynaklanan dış kuvvet, kütle merkezinden geçecek şekilde etki eder ve bunun sonucu olarak da kütle merkezine dış tork etki etmez. Bu yüzden, kütle merkezine göre açısal momentum korunmalı, yani, IiWi = IsWs olmalıdır. Örneğin, bir gösterici, açısal hızını iki katma çıkarmak istediğinde, eylemsizlik momentini ilk değerin yarısına indirmek zorunda kalır.