Merhaba arkadaşlar bu yazımızda Açısal Momentum Nedir, Parçacığın Açısal Momentum ‘u ve Parçaçıklar Sisteminin Açısal Momentum ‘unu sizlere anlatacağım ve örneklerle konuyu kavramanıza yardımcı olacağım. Donmuş bir gölet üzerindeki buza gömülü sağlam bir kazık düşünün (Şekil 1). Bir buz patencisi, yönü çarpmayacak şekilde ayarlayarak bu kazığa doğru hızla kayıyor. Patenci, kazığın yakınındaki bir noktaya yaklaştığında elini uzatarak kazığı yakalıyor ve kazığın çevresinde dairesel bir yol üzerinde hızla dönmeye başlıyor. Doğrusal momentum kavramını öteleme hareketini incelerken nasıl kullandıysak, onun dönme hareketindeki karşılığı olarak da açısal momentum kavramı yukarıda sözü edilen patencinin ve dönme hareketi yapan diğer cisimlerin davranışını anlatmakta bize yardımcı olur.
Patencinin hareketini incelemek için; onun kazığa göre yeri yanında kütlesini ve hızını da bilmemiz gerekir. Daha genel kavramlarla, r vektör konumunda bulunan m kütleli bir cismin, v doğrusal hızıyla hareket ettiğini düşünelim (Şekil 2).
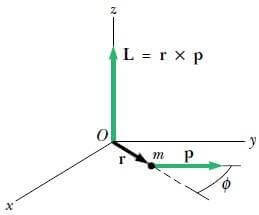
O koordinat başlangıcına göre bir parçacığın L açısal momentumu, o andaki r konum vektörü ile p doğrusal momentumunun vektörel çarpımı olarak tanımlanır:
L = r X p (eşitlik 1)
Açısal momentum ‘un SI birim sistemindeki birimi kg.m2 /s’dir. L’nin büyüklük ve doğrultusunun koordinat başlangıcının seçimine bağlı olduğunu unutmamak gerekir. L’nin doğrultusu, r ve p tarafından oluşturulan düzleme diktir ve yönü sağ-el kuralına göre tayin edilir. Örneğin, Şekil 2’de, r ve p vektörlerinin xy düzleminde olduğu varsayılmıştır. Bu yüzden, L, z doğrultusunda yönelir, p = mv olduğundan, L’nin büyüklüğü
L= mvr sinΦ (eşitlik 2)
eşitliğiyle verilir. Burada Φ, r ve p arasındaki açıdır. r, p’ye paralel olduğunda (Φ =0 veya 180°), L = 0 olduğu görülür. Bir başka deyişle, parçacık başlangıç noktasından geçen bir doğru boyunca hareket ettiğinde, başlangıç noktasına göre sıfır açısal momentuma sahip olur. Öte yandan, r, p ye dikse ( Φ = 90°), o zaman L = mvr olur. Bu durumda, parçacık tam olarak, sanki r ve p tarafından belirlenen düzlem içindeki başlangıç noktası etrafında dönen bir tekerleğin mili üzerindeymiş gibi hareket eder.
Bir parçacığın doğrusal hareket yapması durumunda, parçacığa etki eden bileşke kuvvetin, cismin doğrusal momentumunun zamana göre değişme hızına eşit yani, ∑F = dp/dt olduğunu biliyoruz. Şimdi ise, bir parçacığa etki eden bileşke dönme momentinin, o cismin açısal momentumunun zamana göre değişme hızına eşit olduğunu göstereceğiz. Parçacığa etki eden dönme momentini
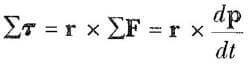
şeklinde yazarak işe başlayalım. Şimdi 1 Eşitliğinin zamana göre türevi alınırsa,
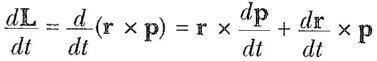
elde edilir. A x B = -BxA olduğu için, yukarıdaki ifadede, vektörel çarpımdaki terimlerin sırası önemlidir. Yukarıdaki ifadede, v = dr/dt, p = mv (vektörel çarpımın 2. özelliği)ye paralel olduğundan, eşitliğin sağındaki son terim sıfır olur. Bu yüzden,
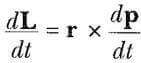
elde edilir. 3 ve 4 Eşitliklerini karşılaştırarak,
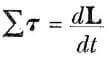
olduğunu görürüz. Bu ifade, Newton’un ikinci yasası olan ∑F = dp/dt ’nin dönme hareketindeki benzeridir. Dönme hareketi ile ilgili olarak 5 eşitliğiyle verilen sonuç,
bir parçacığa etki eden net tork (dönme momenti), parçacığın açısal momentumunun zamana göre değişimine eşit olduğunu ifade eder. 5 eşitliğinin sadece ∑τ ve L vektörlerinin aynı başlangıç noktasına göre ölçülmeleri durumunda geçerli olduğuna dikkat çekmek yerinde olur. (Doğal olarak, aynı başlangıç noktası torkların her biri hesaplanırken de kullanılmalıdır). Dahası, bu ifade, eylemsiz koordinat sistemindeki, sabit herhangi bir başlangıç noktası için de geçerlidir.
Parçacıklar Sisteminin Açışal Momentum ‘u
Bir parçacıklar sisteminin verilen bir noktaya göre L toplam açısal momentumu, parçacıkların her birine ait, açısal momentumların vektörel toplamı olarak tanımlanır:
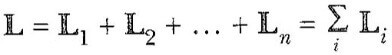
Burada vektörel toplam, sistemdeki n tane parçacığın tamamı üzerindendir.
Parçacıkların her birinin momentumları zamanla değişebileceğinden, toplam açısal momentum da zamanla değişebilir. Gerçekte, 4 den 5’e kadar olan eşitliklere göre, toplam açısal momentumun zamana göre değişiminin, parçacıklar arasındaki iç kuvvetlerden ve parçacıklara etki eden dış kuvvetlerden kaynaklanan torkların tümünün vektörel toplamına eşit olduğunu buluruz. Fakat, iç kuvvetlerden kaynaklanan net tork sıfırdır. Bunun ne ifade ettiğini anlamak için, sistemin oluşturan parçacıklar arasındaki iç kuvvetlerin eşit büyüklükte ve zıt işaretli çiftler halinde bulunduklarını söyleyen Newton’un üçüncü yasasını hatırlayınız. Bu kuvvetlerin, parçacıkların her çiftini birleştiren doğru boyunca uzandıklarını varsayarsak, o zaman, her etki-tepki kuvvet çifti tarafından oluşturulan tork sıfır olur. Yani, 0 başlangıç noktasından kuvvetlerin etki ettiği doğrultuya olan uzaklık olan d moment kolu her iki parçacık için de aynıdır. Özet olarak, parçacıklar sisteminin net iç dönme momentinin sıfır olduğunu görürüz. Son olarak, toplam açısal momentumun sadece, sistem üzerine etki eden net bir dış tork bulunduğunda zamanla değişebileceği sonucuna varırız. Böylece
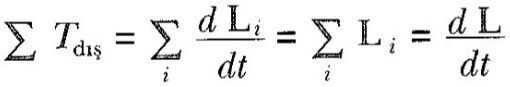
elde edilir. Yani,
eylemsiz bir referans sisteminde, verilen bir orijine göre sistemin toplam açısal momentumunun zamana göre değişimi, o orijine göre sistem üzerine etki eden net dış torka eşittir.
Yukarıdaki 6 Eşitliği, parçacıklar sistemi için verilmiş olan ∑Fdış = dp/dt ifadesinin dönme hareketindeki benzeridir.