Dijkstra Algoritması

Navigasyon nedir ?
Navigasyon yada Türkçe karşılığı ile “Yol Kılavuzu” bulunulan noktadan gidilmek istenilen nokta için en kısa ve en hızlı yolu hesaplayabilen elektronik cihazdır. 90’ lı yılların sonlarına doğru Avrupa’ da yaygınlaşan navigasyon cihazları Türkiye’ ye 2005 yılının sonlarına doğru gelmiştir.

Kısa yolun bulunması :
Navigasyon cihazları iki nokta arasındaki kısa yolu hesaplayabilmek için Hollanda’ lı Matematikçi Dijkstra tarafından bulunan Dijkstra Algoritması’nı kullanırlar. Bu algoritmanın temeli çizge teoremine (Graf Teorisi) dayanır. Kısa yol probleminde harita üzerindeki yerleşim yerleri (iller/ilçeler/köyler vb.) nokta olarak ve bu noktalara giden yollar çizgiler halinde ifade edilmektedir.

Dijkstra Algoritmasının sözde kodu (pseudocode):

1. Başlangıç noktasını belirle.
2. Başlangıç noktasından diğer noktalara olan maliyeti belirle ve düşük maliyetli
   noktayı işaretle.
3. İkinci adımda işaretlenen noktadan gidilebilen diğer noktalar arasında da
   aynı işlemi tekrarla.

Dijkstra Algoritması Örnek

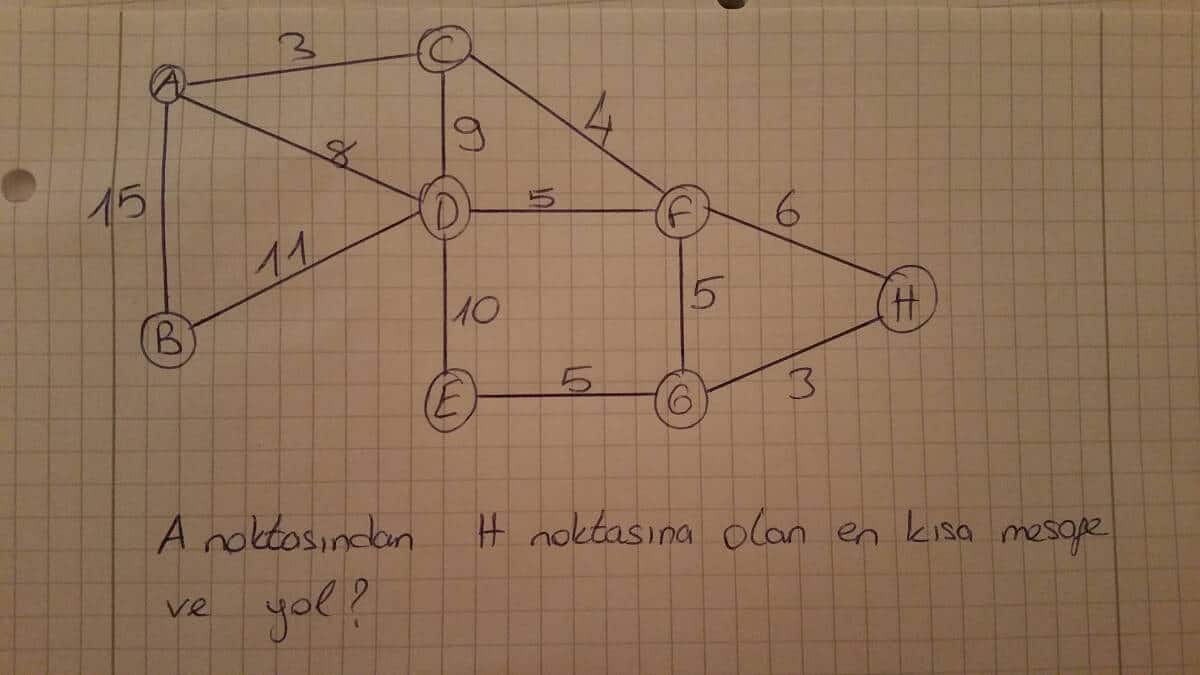
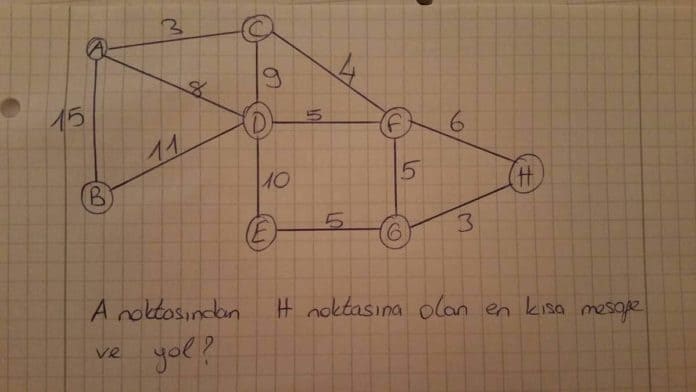
Resimde verilen çizgede A noktasından H noktasına olan en kısa yolu ve yolun maliyetini bulalım.

Dijkstra Algoritması için yukarıdaki resimdeki gibi bir tabela oluşturalım. Tabelanın en solundaki sütun noktaları temsil etmekte ve “pred” sütunu bulunulan noktaya hangi noktadan gelindiğini göstermektedir. “init” sütunu ise algoritmanın başlangıcındaki değerleri göstermektedir.

Başlangıçta bilinen tek bilgi A noktasında bulunulduğudur. Bulunulan noktadan tekrar aynı noktaya gitmenin maliyeti olmadığı için “init” sütununda A’nın değeri 0’ dır. A’ dan diğer noktalara olan uzaklıklar bilinmediği için bu noktaların maliyeti sonsuzdur.

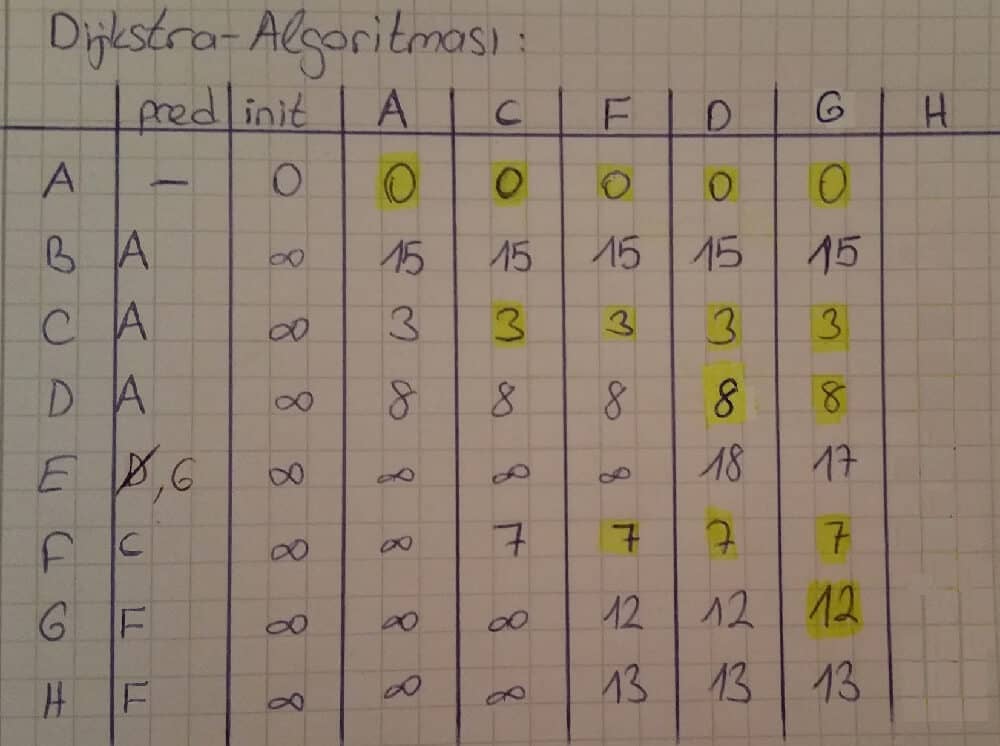
0 herzaman ∞’ dan küçüktür. Bu yüzden yeni oluşturulacak sütun A sütunu olur ve 0 değeri işaretlendiği için sarı renkli kalemle üzerinden geçilmiştir. A-B yolunun maliyeti 15 birim, A-C yolunun maliyeti 3 ve A-D yolunun maliyeti 8 birimdir. A noktasından E, F, G ve H noktalarına direkt geçiş olmadığı için ∞ değerini alırlar. “init” sütununda B, C ve D noktalarının maliyetleri sonsuz olarak belirlenmiştir. Ancak A noktasından bu 3 noktaya daha ucuz maliyetli yol bulunduğu için bu noktaların “pred” sütunundaki karşılığı A olur.

Bir sonraki adımda A sütununda bulunan ve işaretlenmemiş en düşük maliyetli nokta bulunur. Bu nokta 3 birim ile C noktasıdır.

Yeni oluşturulan sütun C sütunudur ve C noktasının maliyeti olan 3 işaretlenir. Ardından işaretlenen değerler (0 ve 3) C sütununa alınır. Bir önceki adım C noktası için uygulanır. C noktasından B noktasına direkt geçiş olmadığı için maliyet ∞’ dur ANCAK önceden bulunan 15 birimlik maliyet ∞ maliyetten düşük olduğu için bu noktanın değeri 15 olarak kalır. C-D arası maliyet 9 birimdir. A noktasından C noktasına gelmek için 3 birimlik maliyet kullanıldı.
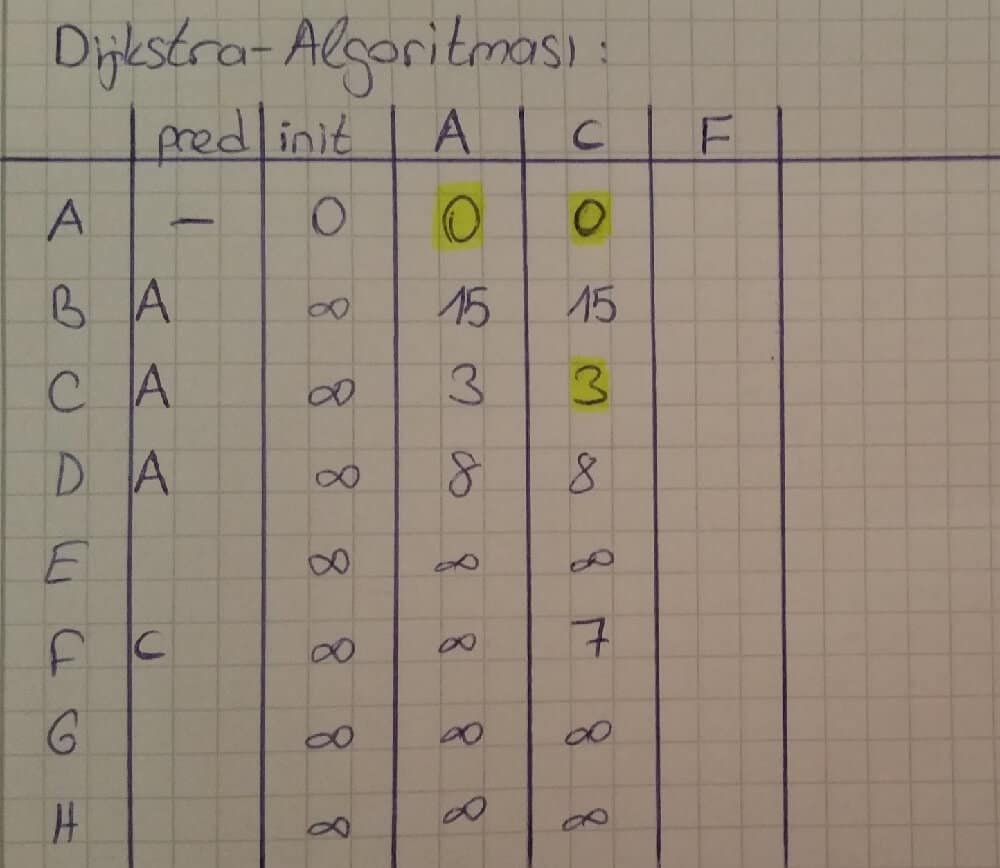
Yani C-D arası yeni maliyet 3 + 9 = 12 birimdir. Bir önceki adımda bulunan 8 birimlik maliyet 12 birimden küçük olduğu için 8 birimlik maliyet yenilenmez ve “pred” sütununda bir değişiklik yapılmaz. C-E, C-G ve C-H noktaları arasında direkt geçiş olmadığı için maliyetleri ∞ olur. Ancak C-F arasındaki yeni maliyet 3 + 4 = 7 birim olarak belirlenir ve 7 birim ∞ birimden küçük olduğu için F’ nin maliyet karşılığına 7 yazılır. F noktasına C noktasından daha düşük maliyetle gidilebildiği için F’ nin “pred” sütunundaki karşılığı artık C noktası olur. C sütunundadki işaretlenmemiş diğer düşük maliyet F’ ye ait olduğu için yeni sütun F sütunu olacaktır.

Yeni oluşan sütunda kullanılan noktalar işaretlenmiştir. Diğer sütunlarda olduğu gibi F noktasından diğer noktalara olan yeni maliyetler hesaplanır. Resimde görüldüğü üzere F noktasından G ve H noktalarına daha düşük maliyetli yollar bulunmuştur. Bu yüzden G ve H noktalarının maliyetleri yenilenmiş ve “pred” sütununa da F noktası yazılmıştır. Algoritma’nın bir sonraki adımında tabela tekrar yenilenir ve ortaya aşağıdaki tabela çıkar:

Bu adımda D noktasının işaretlenmemiş komşu noktalarına olan yeni maliyetleri hesaplanır. A, C ve F noktaları işaretlendiği için bu noktalara olan yenimaliyet tekrardan hesaplanmaz. D noktasına komşu olan ve işaretlenmeyen 2 nokta vardır. Bunlar B ve E noktalarıdır. D noktasından E noktasına olan maliyet 8+10 = 18 birimdir (A-D maliyeti 8 birim, D-E maliyeti 10 birim) ve 18 birimlik maliyet ∞ maliyetten daha az olduğu için E nin yeni maliyeti 18 birim olur ve E’ nin “pred” sütunundaki karşılığı D noktası olur.

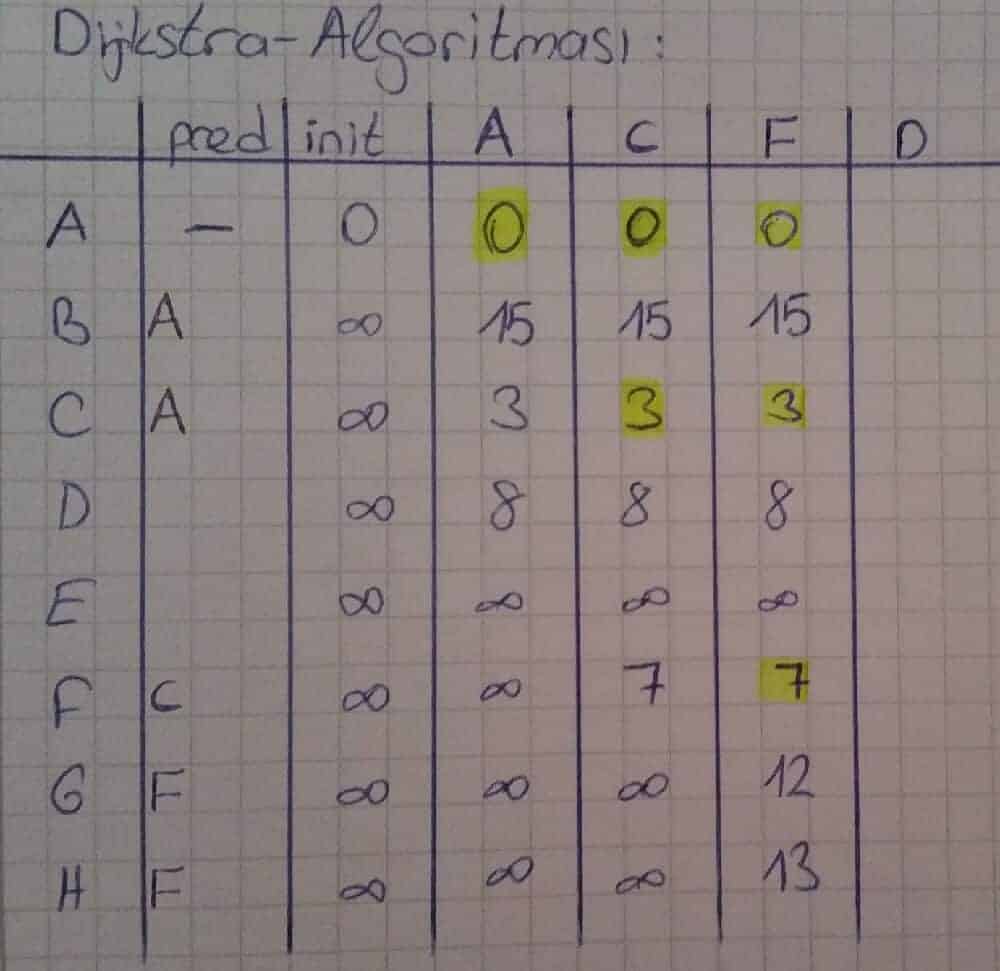
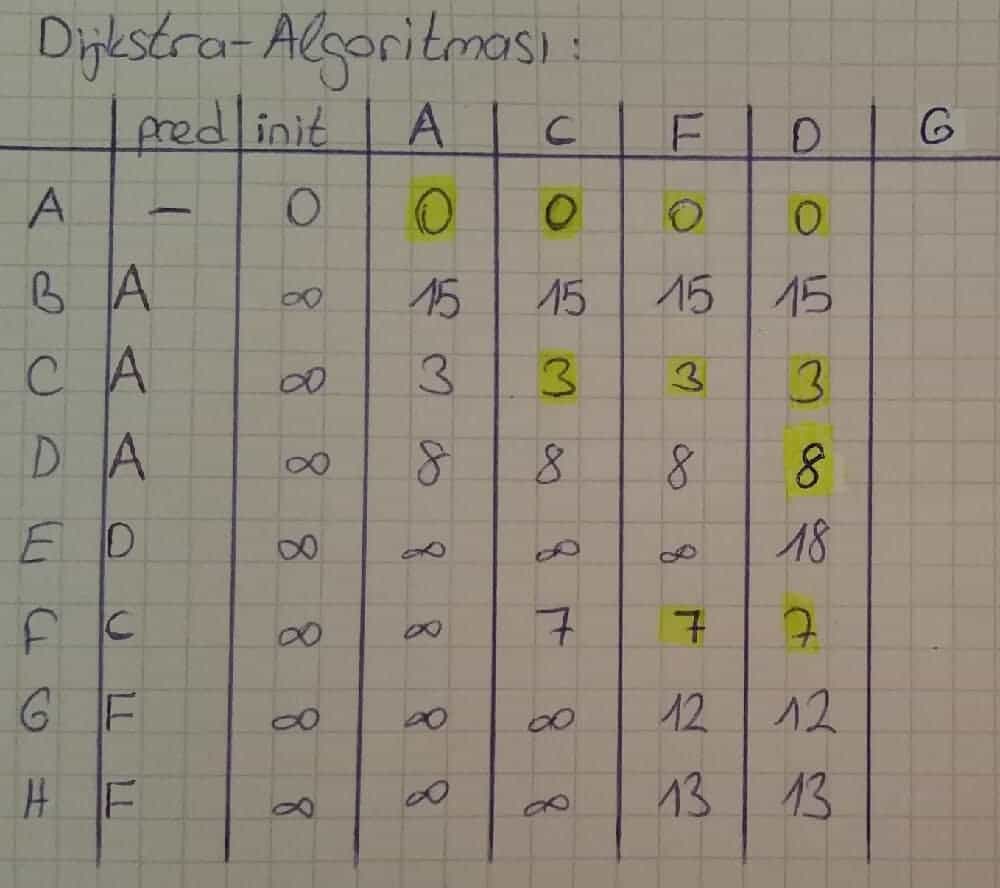
D noktasının komşularına olan yeni maliyetleri hesaplandıktan sonra D sütunundaki işaretlenmemiş en düşük maliyetli nokta için yeni sütun oluşturulur (G sütunu).

Oluşturulan bu sütuna önceden işaretlenmiş noktaların ve G noktasının maliyeti yazılır ve tekrardan işaretlenir. Diğer noktalarda olduğu gibi G noktasının daha önceden işaretlenmemiş komşu noktalarına olan yeni maliyetleri hesaplanır. Burada dikkat çeken nokta D-E mesafedir. Önceden 18 birimlik olan mesafe G noktası üzerinden gidildiğinde 1 birim azalmaktadır, bu sebepten dolayı E noktasının “pred” sütunundaki önceki karşılığı silinir ve yeni karşılığı olan G
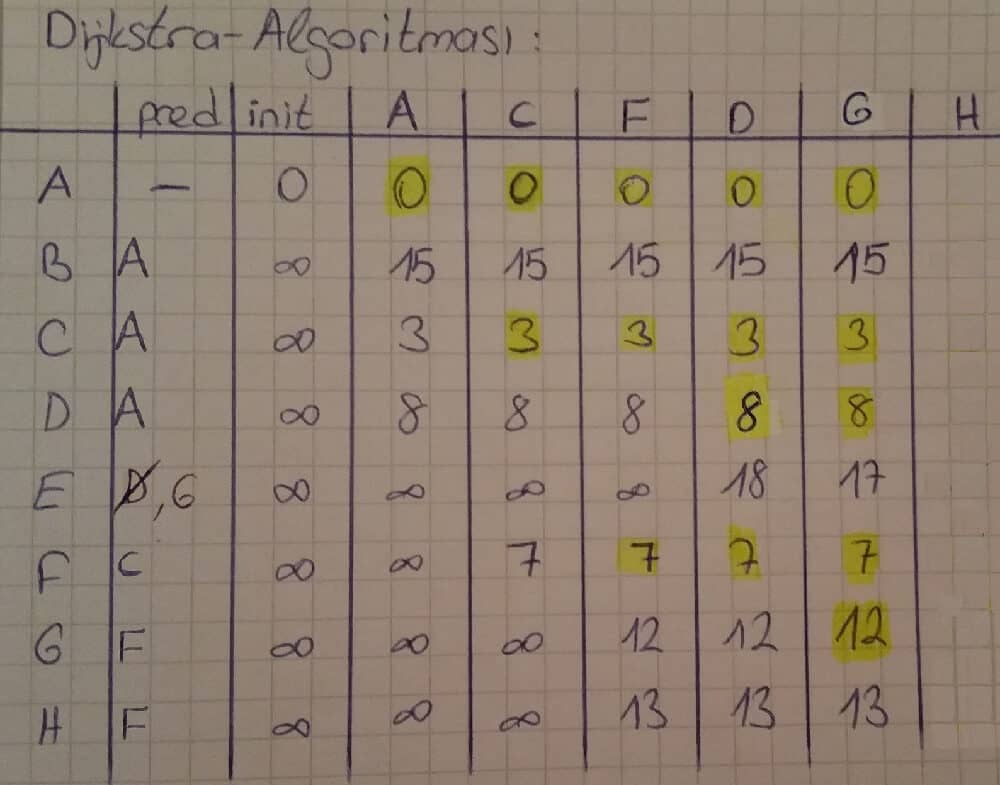
noktası not edilir. Bu şekilde kalan noktalar için de aynı adımlar tekrarlanır.

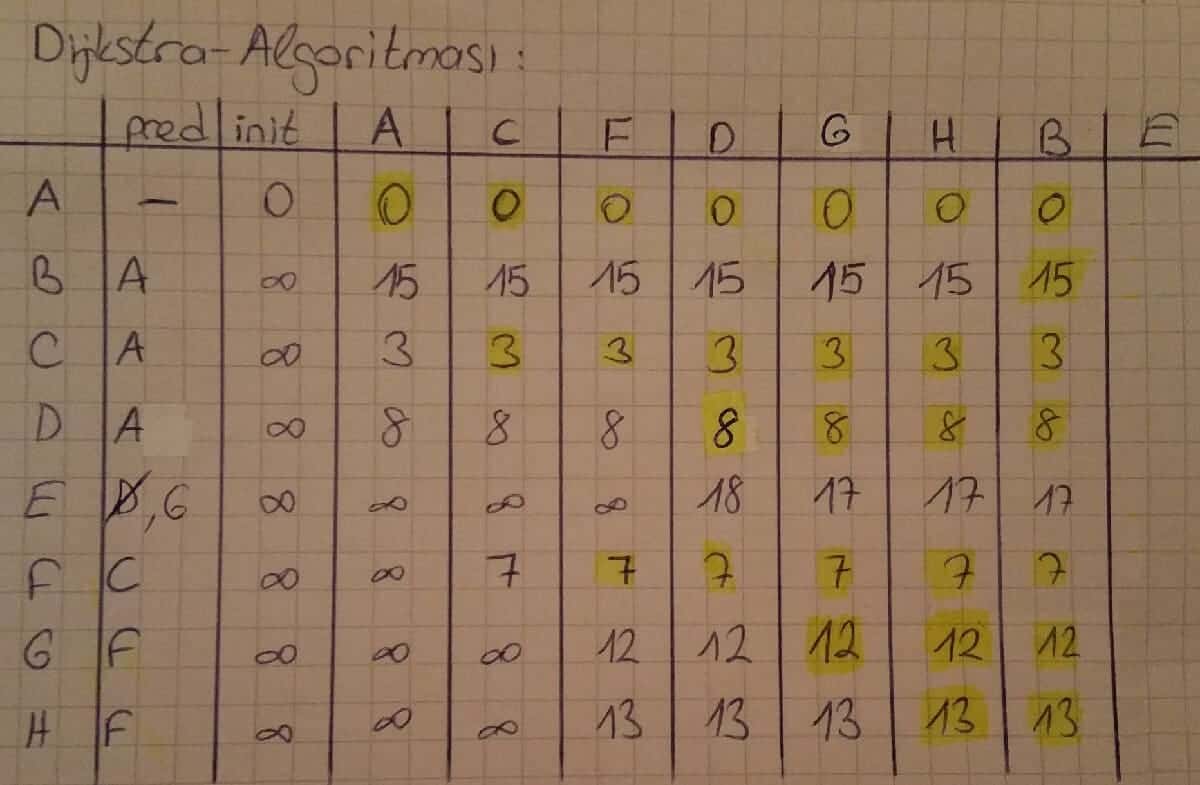
Bu şekilde tüm noktalar için Dijkstra Algoritması uygulandığında aşağıdaki tabela oluşmaktadır.

Bu tabeladan tüm noktaların A noktasına olan en kısa mesafeleri ve bu mesafelerin maliyetleri okunabilir. Örneğin A noktasından H noktasına giden en kısa yolu bulmak için hedef noktasından başlanılarak başlangıç noktasına ulaşılana kadar tüm “pred” karşılıkları not edilir. H’ nın pred karşılığı F, F’ nin pred karşılığı C, C’ nin pred karşılığı başlangıç noktası olan A.

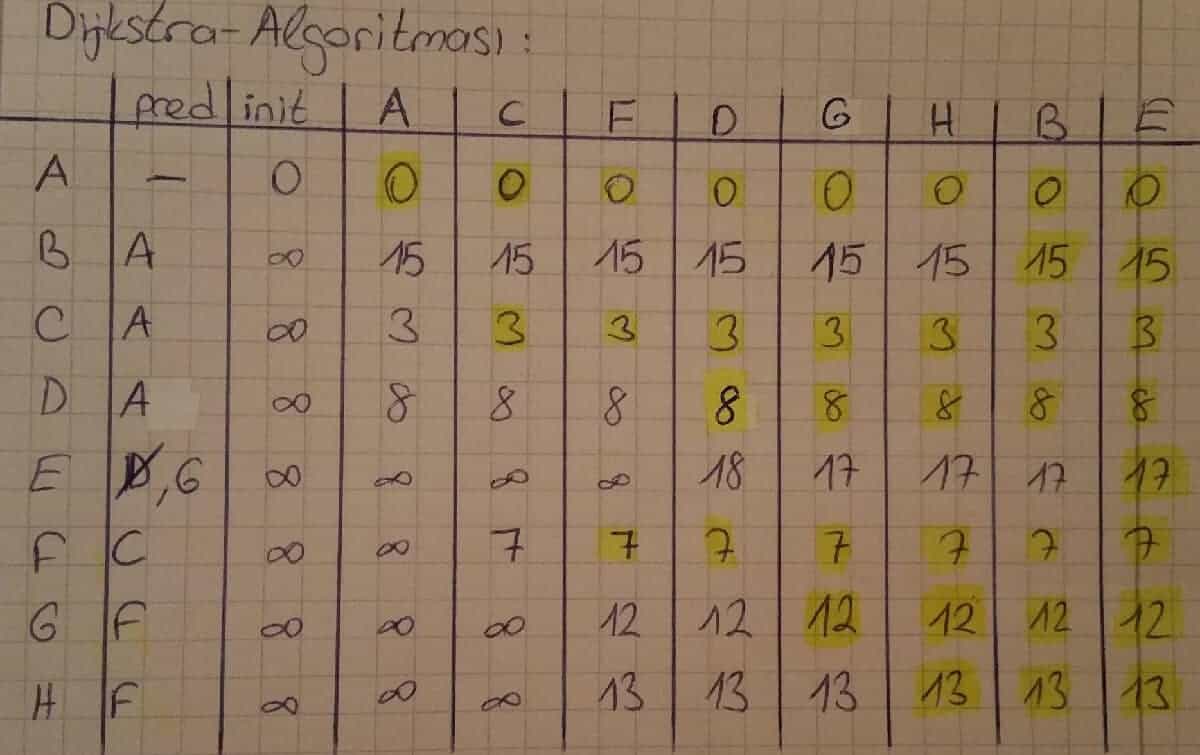
A-H kısa yolu: A → C → F → H
A-H kısa yolu maliyeti: 12 birim.
A noktasından E noktasına olan en düşük maliyetli yol:
E’ nin pred karşılığı G, G’ nin pred karşılığı F, F’ nin pred karşılığı C ve C’ nin
pred karşılığı A.
Kısa yol: A → C → F → G → E
Maliyet: 17 Birim