Bu problem aslında herhangi bir pazar gazetesinin bulmaca ekinde bulacağınız tarzda bir soru. Bir savaş olduğunu düşünün. Her biri 6 farklı rütbeli subay içeren altı alaydan oluşan bir ordunun başındasınız. Soru şöyle: 6’ya 6 ‘lık bir kareye her bir subayı farklı rütbelerde olacak şekilde yerleştirebilir misiniz?
Bu soruyu ünlü yapan ise matematik dünyasının “babası” denilecek yeterliliklere sahip Euler’in üzerinde çalışmasından kaynaklanmaktadır. Euler böyle bir çözümün olamayacağını belirtmiş ve çözümün olmasının imkansız olduğunu göstermiştir. Fakat Eulerin yaptığı karalamadan başka bir şey değildi. Problemin çözümünün olamayacağını resmi olarak 130 yıl sonra Fransız matematikçi Gaston Terry ispatladı ve aynı yıl yani yıllar 1901’i gösterdiği zaman da bir dergide yayınladı.
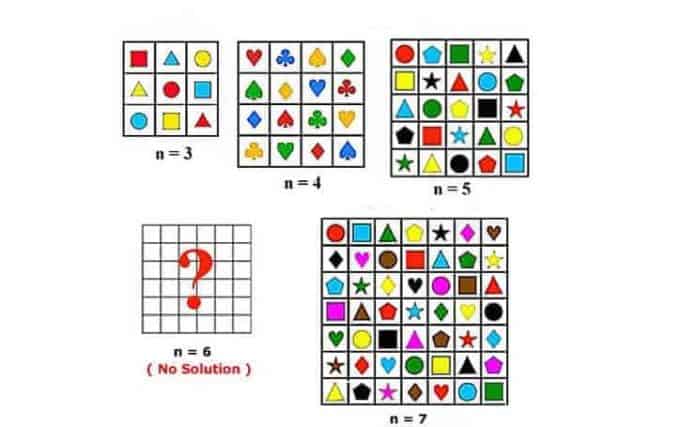
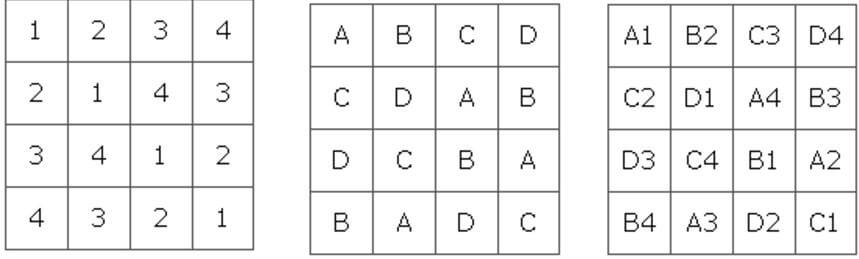
Latin karelerinden geçtiyseniz ki bu kareler önemli tarihi eser niteliğinde eserlerdir, 36 subay sorununu size hatırlatacaktır. Latin kareleri her sembolün her satır ve sütunda bir kez belirdiği özel bir kare çeşididir. (örneğin sayı veya harf). Aynı büyüklükte fakat farklı simgelerle iki Latin karesini birleştirirseniz, Graeco-Latin kare (ayrıca Euler kare olarak da adlandırılır) adında yeni bir kare oluşturmuş olursunuz. Bu kare bir çift simgeyi içerir, böylece bir çiftin her üyesi her satır ve sütunda tam olarak bir kez oluşur ve böylece her olası çift dizide tam olarak bir kez görünür. Hemen aşağıdaki gibi uyarlayabiliriz.
Peki neden matematik dünyası bu problemin çözümünün ve adımlarının hepsini Euler’e ithaf etti. Matematikçi Terry bu yapılan çalışmayı yayınlayan ve makale haline getiren kişi değil mi? Sorunun cevabı matematik tarihçileri için şöyle; Euler zamanın ve yüzyılın çok ötesinde bir matematikçiydi. Ona bu tip sorular mektupla, onlarca hatta yüzlerce kez geldi ve en uzun olan düşünmesi 2 saatini geçmeyecek biçimde cevapladı. Belki de bu sorular onun için bir anlam ifade etmiyordu. Kim bilir? Bu sorunun tüm çözümlerini Leonhard Euler biliyordu hatta kare sayısının hangi koşullar altında subayların tek tek dizileceğini dahi göstermişti. Bu yüzden ilk mimar ve düşünce sahibi o idi.
36 subay sorunu, günümüzdeki sudokulara benzer sorunlar da dahil olmak üzere Latince ve Graeco-Latin karelerinde çok fazla çalışma yapmaya ilham kaynağı oldu. Tahmin edebileceğiniz gibi, nesneleri belirli kısıtlamalar altında karşılayacak şekilde birleştirmeyi ve gerçek dünyada birçok uygulamaya sahip olan kombinasyon denilen bir matematik alanına önemli bir katkıda bulundu.